Unlocking single cell spatial omics analyses with scdney

## library(devtools)
## library(BiocManager)
library(SingleCellExperiment)
library(ggplot2)
library(scFeatures) ## devtools::install_github("SydneyBioX/scFeatures")
library(ClassifyR) ## BiocManager::install("ClassifyR", dependencies = TRUE)
library(lisaClust) # BiocManager::install("lisaClust")
library(ggthemes)
library(spicyR) ## BiocManager::install("spicyR")
library(dplyr)
library(limma)
library(plotly)
library(scattermore)
library(tidyr)
library(survival)
library(survminer)
library(spatstat)
library(scater)
library(scran)
library(reshape)

theme_set(theme_classic())

# code for plotting purpose
plot_boxplot <- function( feature ){
  
  data_plot <- t(feature)
  data_plot <- melt(data_plot )
  
  colnames(data_plot) <- c("X1", "X2", "value")
  data_plot$condition <- unlist( lapply( strsplit(  as.character( data_plot$X2), "_cond_"), `[`, 2))
  
  p <- ggplot(data_plot, aes( x = X1, y = value , colour = condition)) + 
    geom_boxplot()  + 
    theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust=1))
   
  return(p)
}
  

plot_barplot <- function(data , dodge=F  ){

  data$patient <- unlist( lapply( strsplit( rownames(data ), "_cond_"), `[`, 1))
  data$condition <- unlist( lapply( strsplit( rownames(data ), "_cond_"), `[`, 2))
  
  data <- as.data.frame( melt(data, id=c("patient", "condition")) )
 
  p <-   ggplot(data , aes( x = patient , y = value , fill = variable) ) +   
    geom_bar(stat="identity"   ) + facet_wrap(~condition, scale="free") + 
    theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust=1)) 
 
 return (p)
}


 
draw_dotplot <- function(data_sce, sample, celltype , group , group_of_interest ){

  df <- data.frame(colData( data_sce))
  # for each patient, calculate the proportion of each cell type in each region.  

  df_plot <- NULL
  for ( thispatient in unique(df[[sample]])){
    this_df <- df[df[[sample]]== thispatient, ]
    temp_df <-   table( this_df$region, this_df[[celltype]] )
    temp_df <-  temp_df / rowSums(temp_df)
     temp_df <- data.frame(  temp_df)
    temp_df$patient <-  thispatient
    temp_df$group <- clinical[clinical[[sample]] == thispatient,  group ]  
    df_plot <- rbind(df_plot, temp_df)
  }
  
  # for each region, calculate the average proportion of each cell type across all individuals 
  df_plot <- df_plot %>% dplyr::group_by( Var1 , Var2, group) %>% 
    summarise(mean_proportion = mean(Freq))
    
  # we are only interested in the short term and long term survival individuals 
  df_plot  <- df_plot [ df_plot$group %in% group_of_interest, ]
   
  p <- ggplot(df_plot, aes(y = Var2, x = Var1 ,colour =mean_proportion  , size = mean_proportion ))+  
    geom_point() + 
    facet_grid(~group, scales = "free", space = "free" ) + 
    theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust=1)) + 
    xlab("Region" ) + ylab("Cell type") + scale_colour_viridis_c()
  
  return(p)
}

draw_region_clustering_result <- function( data_sce, sample , selected_sample   ){
  # get meta data for a selected patient to visualise 
  metadata <- colData(data_sce)
  metadata <- metadata[metadata[[sample]] == selected_sample ,  ]
  metadata <- data.frame(metadata)

  
  plotlist <- list() # define the list to store images for region highlighting 
  plotlist_celltype <- list() # define the list to store images for cell-type highlighting 
   
  # optional: define a colour palette
  # you can also specify your own colour to use in the variable color_codes 
  tableau_palette <- scale_colour_tableau( palette = "Tableau 20") 
  color_codes <- tableau_palette$palette(18)
  color_codes <- c(color_codes, "darkgrey")  # for all other regions apart from region of interest, make the colour grey 
  names(color_codes) <- c(unique(metadata$description) ,  "other regions")
  
  
  # look through each region to highlight the region of interest, as well as the cell type in the region of interest
  for ( thisregion in sort(unique(metadata$region))){
      
        # select the region of interest
        selected_region_index <-  metadata$region == thisregion
        
        # for all other regions, define them as "other regions" so that they will be greyed out 
        metadata$selected_region <-  "other regions"
        metadata$selected_region[selected_region_index] <- "selected region"
        
        # for all cell types outside the region of the interest, also make them greyed out 
        metadata$celltype <- metadata$description
        metadata$celltype[!selected_region_index ] <-   "other regions"
        metadata$celltype <- factor(metadata$celltype, levels = c(unique(metadata$description), "other regions"))

        # plot ggplot highlighting the region of interest
       p <- ggplot(metadata, aes(x = Location_Center_X , y = Location_Center_Y , colour = selected_region  )) + geom_point(alpha = 0.7) + ggtitle(thisregion) + scale_colour_manual(values = c("grey" , "red"))
         
       # plot ggplot highlighting the cell-types in the region of interest 
       p2 <-  ggplot(metadata, aes(x = Location_Center_X , y = Location_Center_Y , colour =  celltype )) + geom_point(alpha = 0.7 ) + ggtitle(thisregion) + scale_colour_manual(values =  color_codes)
       
      plotlist [[thisregion ]] <- p
       
      plotlist_celltype [[thisregion ]] <- p2
      
  }
  
  a <- ggarrange(plotlist = plotlist , ncol = 5, nrow = 1 , common.legend = T )
  b <- ggarrange(plotlist = plotlist_celltype , ncol = 5, nrow = 1 , common.legend = T )
  
  return (list(a,b))
}


draw_selected_region_boxplot <- function(data_sce, sample , celltype, group ,  group_of_interest, select_region){
  
    df <- clinical[colData(data_sce)[, sample ], ]
   df$region <- data_sce$region
   df[[celltype]] <- data_sce[[celltype]]
  
   df_plot <- NULL
   for ( thispatient in unique(df[[sample]])){
      this_df <- df[df[[sample]] == thispatient, ]
      temp_df <-   table( this_df$region, this_df[[celltype]] )
      temp_df <-  temp_df / rowSums(temp_df)
      temp_df <- data.frame(  temp_df)
      temp_df$patient <-  thispatient
      temp_df$group <- unique( this_df[[group]])
      df_plot <- rbind(df_plot, temp_df)
    }
    
     
  df_plot_region <- df_plot[df_plot$Var1 == select_region , ]
  
    
  df_plot_region  <-  df_plot_region [ df_plot_region$group %in% group_of_interest, ]
   
  p <- ggplot(df_plot_region,  aes(x =  Var2,  y = Freq, colour = group)) +
    geom_boxplot()+ 
    theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust=1))  + 
    ylab("Proportion") + xlab("Cell type") + ggtitle("Selected region") + ylim(0, 0.25)
   
  
  return(p)
 
}

Overview

The recent development of spatial omics allows us to examine the spatial organisation of cells within tissues in their native environment. This workshop will discuss the challenges and analytical skills associated working with multi-sample spatial datasets and their use in disease risk prognosis. We will also introduce general analytical strategies and critical thinking questions that arise in the workflow.

Preparation and assumed knowledge

Knowledge of R syntax
Familiarity with the SingleCellExperiment class
Basic knowledge in single cell data analysis. You can access our previous workshops for a quick review in single cell data analysis.
Ability to install all required R packages, please check sessionInfo at the end of this document to ensure you are using the correct version.
Familiarity with our previous workshop vignette on Introduction to Single Cell RNA-seq Analysis

Learning Objectives

Describe and visualise spatial omics datasets
Calculate different spatial statistics at the cell-type level using scFeatures
Perform multi-view disease outcome prognosis with the package ClassifyR
Understand and perform cell segmentation using BIDCell
Develop an understanding of:
- evaluation of classification and survival models
- evaluate cohort heterogeneity given a survival model
Explore various strategies for disease outcome prognosis using spatial omics data

Note: This data workshop offers participants the opportunity to engage in hands-on analysis using R. However, if you are not comfortable with coding in R, you can still acquire valuable analytical skills by reviewing the output we provide in this file.

Time outline

Structure of the 3-hour workshop:

Activity	Time
Part 1: Introduction	20m
Part 2: Exploring spatial data	30m
Part 3: Feature engineering with scFeatures	30m
Break	15m
Part 4: Survival analysis with ClassifyR	20m
Part 5. Identify cohort heterogeneity	20m
Part 6: Cell segmentation with BIDCell	20m
Concluding remarks	10m

Part 2: Exploring spatial data

Data and background

A subset of the widely-known METABRIC breast cancer cohort has recently been analyzed using imaging mass cytometry: Imaging Mass Cytometry and Multiplatform Genomics Define the Phenogenomic Landscape of Breast Cancer. The question we are asking is: can their risk of recurrence be accurately estimated and therefore inform how aggressively they need to be treated? The other component of the analysis is patient clinical data, which has been sourced from Supplementary Table 5 of Dynamics of Breast-cancer Relapse Reveal Late-recurring ER-positive Genomic Subgroups.

## Quick look at data
assay(data_sce)[1:5, 1:5]

##           MB-0002:345:93 MB-0002:345:107 MB-0002:345:113 MB-0002:345:114
## HH3_total     4.82032390       3.8229411      2.55845170      4.82208870
## CK19          1.21185160       1.3223530      0.13832258      0.33366668
## CK8_18        2.80274720       2.4720588      0.60545164      2.43351100
## Twist         0.14651649       0.1176471      0.09877419      0.20791112
## CD68          0.07863736       0.1016471      0.03225806      0.05237778
##           MB-0002:345:125
## HH3_total      2.41391110
## CK19           0.07055555
## CK8_18         0.20724444
## Twist          0.12004445
## CD68           0.00000000

Basic characteristics of the data objects:
- The dataset contains 38 proteins and 76307 cells.
- The outcome is recurrence-free survival.

Covariates

 data.frame(colData(data_sce)[1:5, ])

##                      file_id metabricId core_id ImageNumber ObjectNumber
## MB-0002:345:93  MB0002_1_345    MB-0002       1         345           93
## MB-0002:345:107 MB0002_1_345    MB-0002       1         345          107
## MB-0002:345:113 MB0002_1_345    MB-0002       1         345          113
## MB-0002:345:114 MB0002_1_345    MB-0002       1         345          114
## MB-0002:345:125 MB0002_1_345    MB-0002       1         345          125
##                 Fibronectin Location_Center_X Location_Center_Y SOM_nodes
## MB-0002:345:93    0.4590055          179.7088          27.90110       130
## MB-0002:345:107   0.1176471          193.0588          29.29412       131
## MB-0002:345:113   0.2512903          162.1935          28.83871        83
## MB-0002:345:114   0.4788444          198.3111          29.15556       128
## MB-0002:345:125   6.1901112          262.8889          31.26667         7
##                 pg_cluster    description   region      ki67
## MB-0002:345:93          54       HR- CK7- region_1  low_ki67
## MB-0002:345:107         54       HR- CK7- region_4  low_ki67
## MB-0002:345:113         28    HRlow CKlow region_1 high_ki67
## MB-0002:345:114         54       HR- CK7- region_4 high_ki67
## MB-0002:345:125         11 Myofibroblasts region_2  low_ki67
##                               celltype  sample   x_cord   y_cord
## MB-0002:345:93        HR- CK7--region1 MB-0002 179.7088 27.90110
## MB-0002:345:107       HR- CK7--region4 MB-0002 193.0588 29.29412
## MB-0002:345:113    HRlow CKlow-region1 MB-0002 162.1935 28.83871
## MB-0002:345:114       HR- CK7--region4 MB-0002 198.3111 29.15556
## MB-0002:345:125 Myofibroblasts-region2 MB-0002 262.8889 31.26667

Summary

At the start of any analysis pipeline, it is often good to explore the data to get a sense of the structure and its complexity. We usually do this by exploring the distribution of the outcomes and variables within the meta-data. Here, we use cross-tabulation to examine the following variables:

Surgery vs death
ER status
Grade

print("Stage and death")

## [1] "Stage and death"

table(clinical$Breast.Surgery, clinical$Death, useNA = "ifany")

##                    
##                      0  1
##   BREAST CONSERVING 38 14
##   MASTECTOMY        16  6
##   <NA>               2  1

print("Number of individuals based on ER status")

## [1] "Number of individuals based on ER status"

table(clinical$ER.Status)

## 
## neg pos 
##  12  64

print("Number of individuals based on Grade")

## [1] "Number of individuals based on Grade"

table(clinical$Grade)

## 
##  1  2  3 
## 14 30 28

Visualise data

Typically in single-cell data analysis, we perform dimension reduction to project the high dimensional cell x gene matrix on to 2D space. This allows us to visualise various things of interest, such as distribution of cell-types and disease outcomes. In this dataset, cells were classified into 22 cell-types based on their markers.

data_sce <- runUMAP(data_sce, scale=TRUE)

# With the UMAP function we can highlight by meta data of interest
# Here we highlight the cell-types and sample ID
a <- plotUMAP(data_sce, colour_by = "description")
b <- plotUMAP(data_sce, colour_by = "metabricId")

ggarrange(plotlist = list(a,b))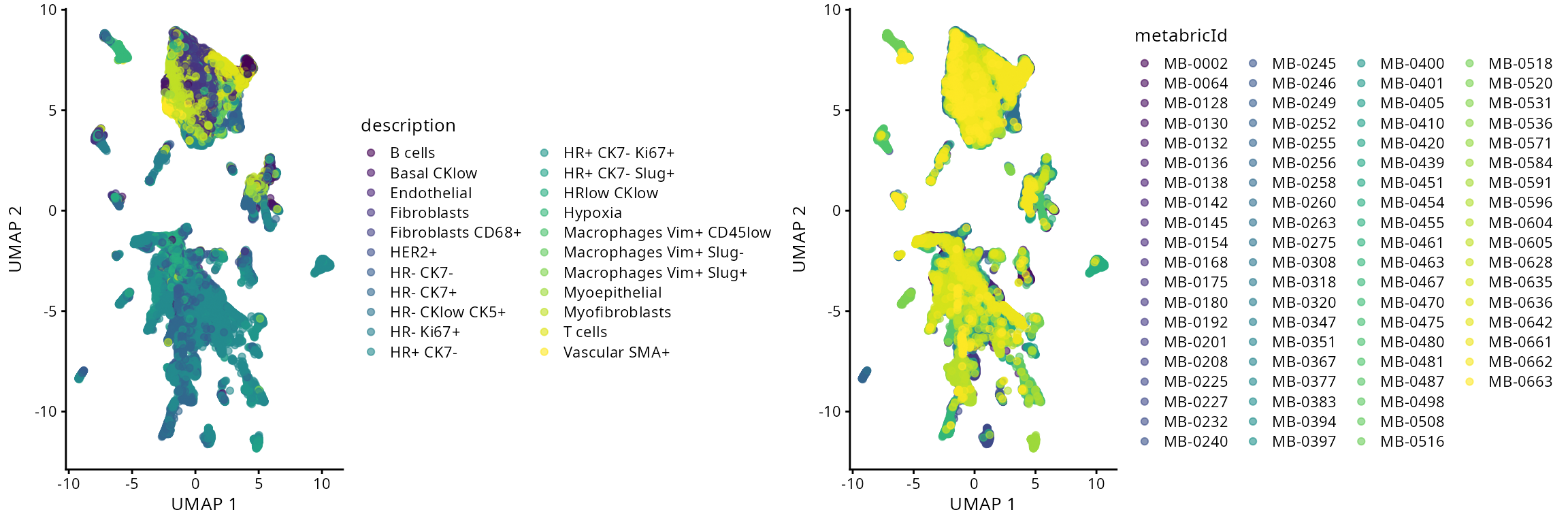

Visualise selected patient:
Here we selectively visualise two individuals by highlighting only the selected individuals.

# Extract the meta data and the UMAP dimension of the dataset
metadata <- colData(data_sce)
metadata <- cbind(metadata, reducedDim(data_sce, "UMAP"))
metadata <- data.frame(metadata)

# For the selected patient MB-0475, denote it as "selected patient" 
# and all other individuals as "other individuals"
metadata$selected_patient <- ifelse(metadata$metabricId == "MB-0475", "seleted patient" , "other individuals")

# Generate a UMAP plot and store it in R object `a`   
a <- ggplot(metadata, aes(x =UMAP1 , y = UMAP2 , colour = selected_patient  )) + geom_scattermore(pointsize = 0.5)  + scale_colour_manual(values = c("grey" , "red"))
 
# For the selected patient MB-0628, denote it as "selected patient" 
# and all other individuals as "other individuals"
metadata$selected_patient <- ifelse(metadata$metabricId == "MB-0628", "seleted patient" , "other individuals")
        
# Generate a UMAP plot and store it in R object `b`   
b <- ggplot(metadata, aes(x =UMAP1 , y = UMAP2 , colour = selected_patient  )) + geom_scattermore(pointsize = 0.5)  + scale_colour_manual(values = c("grey" , "red"))
 
ggarrange(plotlist = list(a,b))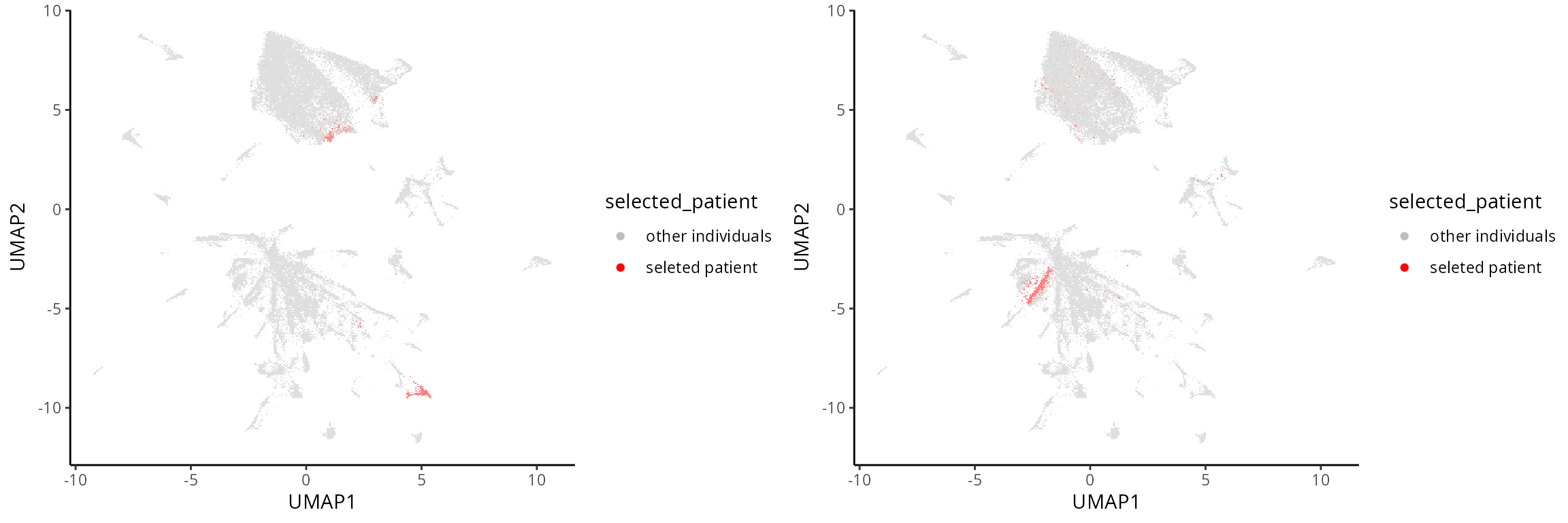

Interactive Q&A:

What can we learn from these illustrations? Is there anything interesting in the plot? Questions to consider include:

Q&A 1: Does each cell-type cluster together?
Q&A 2: When there is a large number of categories, are dimensionality reduction plots interpretable or misleading due to overplotting?

Spatial structure

The advantage with spatial omics is that we can examine the organisation of the cell-types as it occurs on the tissue slide. Here, we visualise one of the slides from a patient. As an optional exercise, you can:
- permute the cell-type label.
- permute the spatial coordinate.
to give a sense of what is random ordering.

We select a particular patient “MB-0002” and visualise its spatial pattern using ggplot.

# obtaining the meta data for this patient 
one_sample <- data_sce[, data_sce$metabricId  == "MB-0002"]
one_sample  <- data.frame(colData(one_sample))
 
ggplot(one_sample, aes(x = Location_Center_X, y = Location_Center_Y, colour = description)) + 
  geom_point(alpha=0.7) + 
  scale_colour_tableau() + 
  ggtitle("Original slide")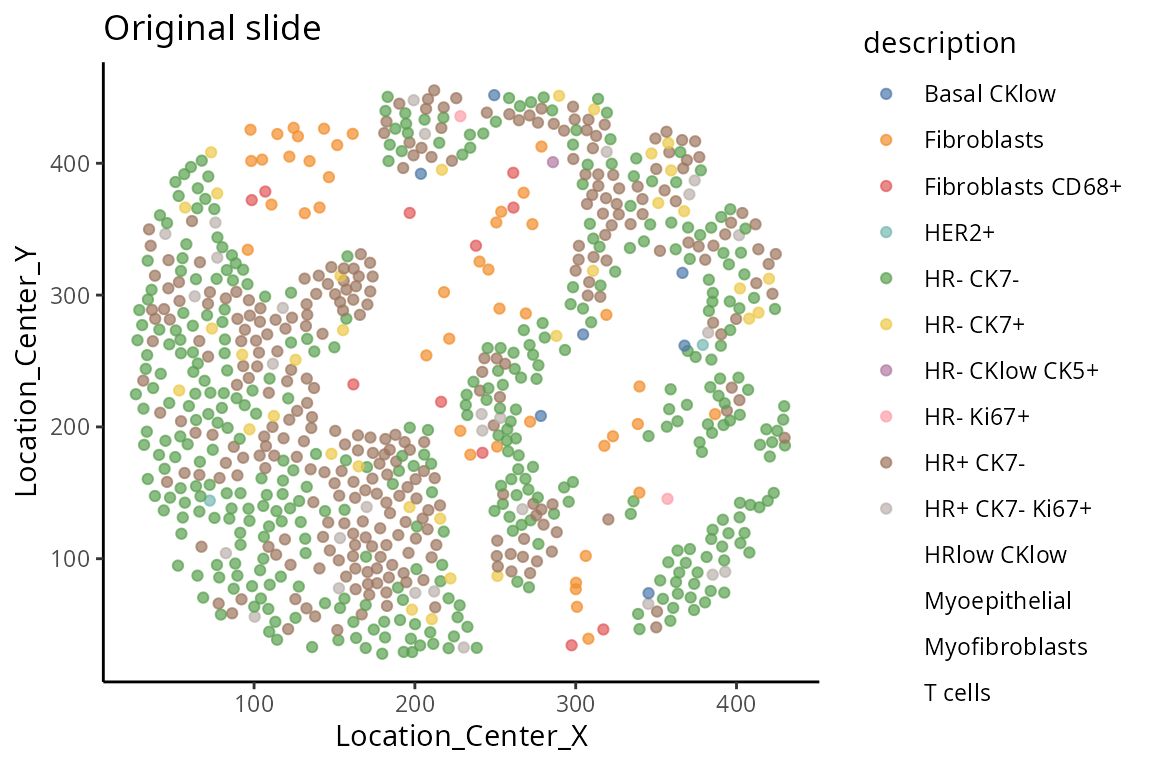

Cellular neighbourhoods

Spatial data allow for the identification of a variety of characteristics including distinct cell-types within an image, providing an overview of the tissue environment. This allows scientists to explore the cellular architecture and environment and its association with phenotype information (e.g meta-data). For our data story, we are interested in whether the individuals have a good or poor outcome. The outcome is often called a ‘prognosis’ and a good outcome is sometimes called ‘favourable’. In this section, we examine graphically how cell-type co-localisation varies across spatial regions and how is such information associated with individual survival outcome.

We begin by examining how can we identify and visualise regions of tissue where spatial associations between cell-types are similar. There are many packages that perform this task and here we use the lisaClust function that is based on “local L-function” to spatially cluster cells into different regions with similar cell-type composition.

This has already been pre-loaded for you. Please proceed to the next task.

set.seed(51773)
BPPARAM <- MulticoreParam(16)

# Cluster cells into spatial regions with similar composition.
data_sce  <- lisaClust(
  data_sce,
  k = 5,
  Rs = c(20, 50, 100),
  sigma = 50,
  spatialCoords = c("Location_Center_X", "Location_Center_Y"),
  cellType = "description",
  imageID = "ImageNumber" ,
  regionName = "region",
  BPPARAM = BPPARAM
)

We have use the lisaClust function in the previous subsection to cluster cells into five different spatial regions. Next, as a case study, we will compare individuals with good or poor prognosis and examine graphically, if any regions appear to be different between good or poor prognosis. We define:
- Good prognosis as individuals with > 10 years recurrence-free survival and
- Poor prognosis as individuals with < 5 years recurrence-free survival.

using the code below and store the information under clinical$survivalgroup. The recurrence free survival (RFS) is provided in the variable timeRFS

## Extract time to recurrence-free survival
clinical$survivalgroup <- "neither"

## Define poor and good prognosis
clinical$survivalgroup[which( clinical$timeRFS  < 5* 365) ] <- "poor" 
clinical$survivalgroup[which( clinical$timeRFS  > 10* 365) ] <-  "good"

Individual level

Here we visualise the spatial domain (regions) detection result based on one individual. We can either visualise all regions in one graph or highlighting each region in separate graphs. Here we will use the terminology “spatial domain” and “regions” interchangeably.

Depending on the number of regions, it may be more useful to visualise the spatial regions either collectively in a single graph or separately in multiple graphs. To visualise it in a single graph, the hatchingPlot() function is used to create hatching patterns for representating spatial regions and cell-types. The hatching geom is used to create hatching patterns for representation of spatial regions.

## To visualise it in a single graph
hatchingPlot(
  data_sce,
  region = "region",
  imageID = "metabricId",
  cellType = "description",
  spatialCoords = c("Location_Center_X", "Location_Center_Y") )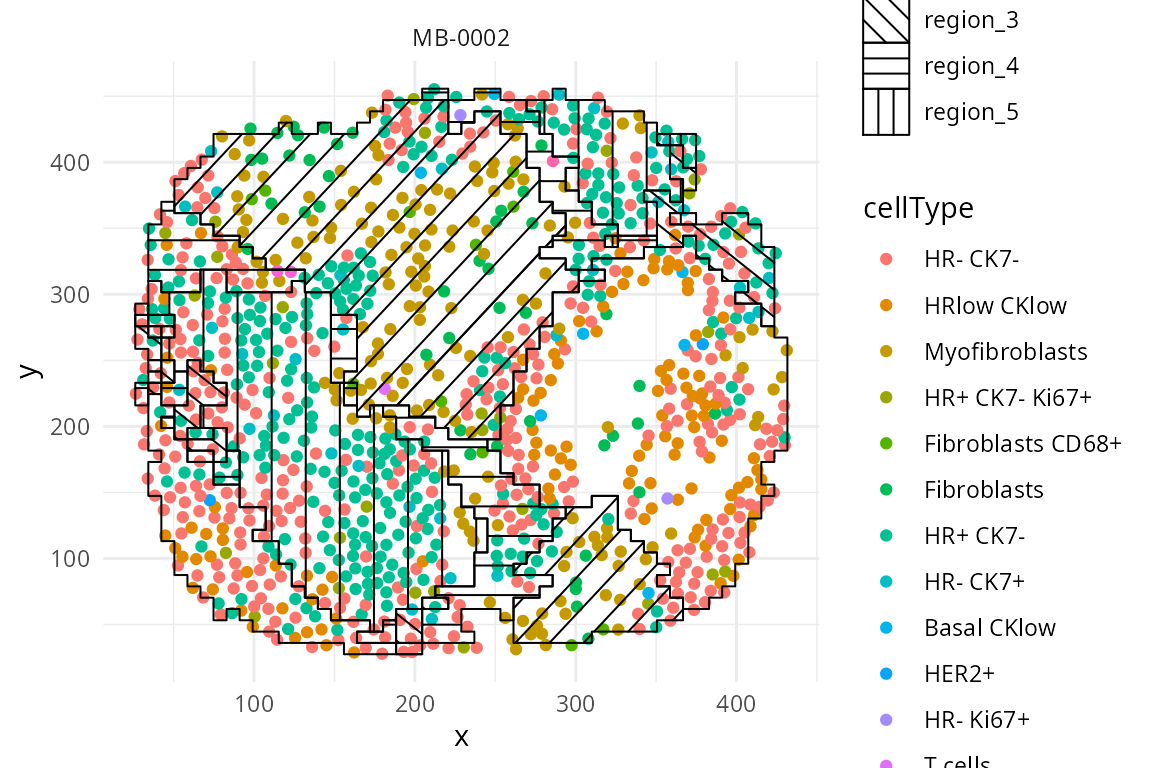

We have written a small function draw_region_clustering_result to visualise the data separately in multiple graphs for the individual MB-0002.

draw_region_clustering_result(data_sce , 
                              sample = "metabricId" , 
                              selected_sample =  "MB-0002" )

## [[1]]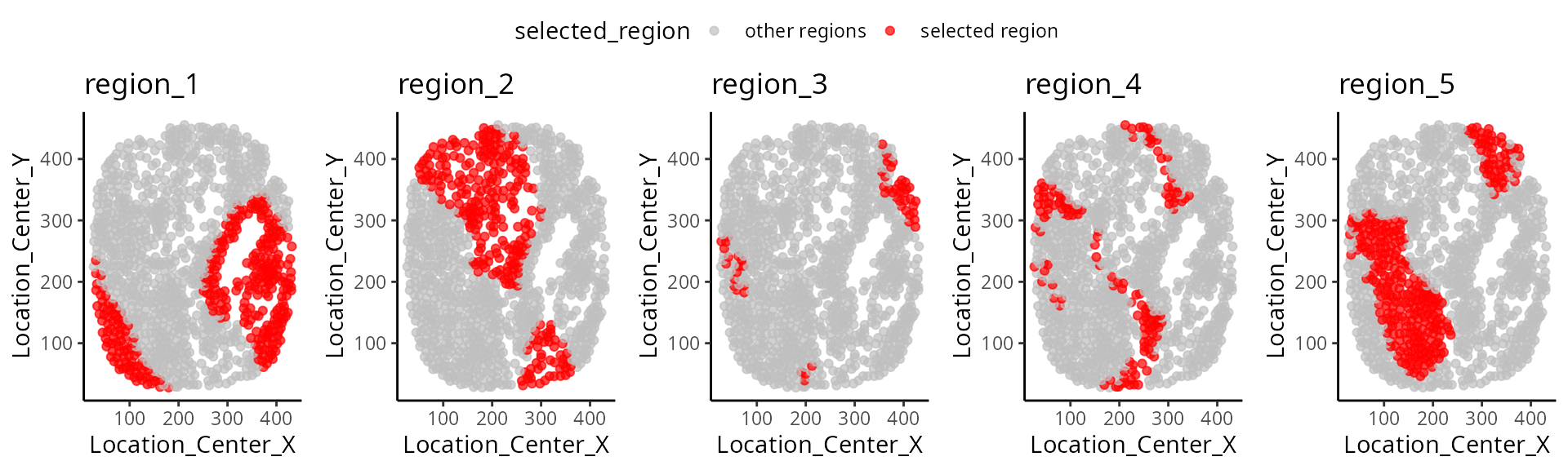

## 
## [[2]]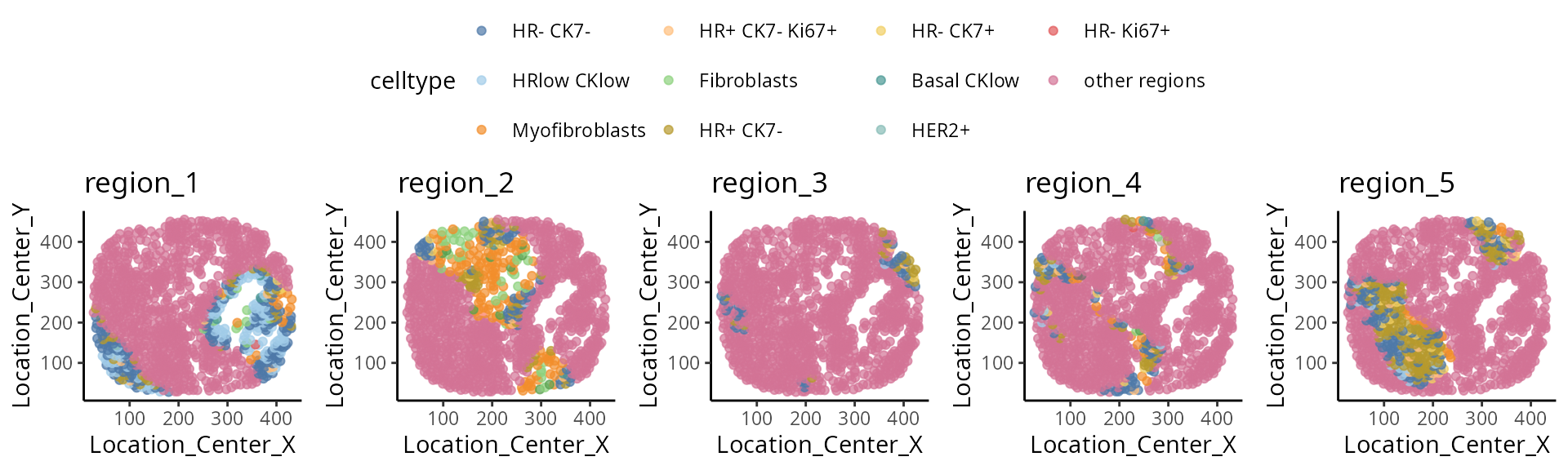

Across individuals

We can better interpret the region output by summarising the proportion of each cell-type in a region across the individuals. We look at the composition of cell-types in each region and compare between prognostic outcomes.

draw_dotplot(data_sce,  
             sample = "metabricId" , 
             celltype = "description" ,  
             group= "survivalgroup" , 
             group_of_interest =  c("poor" , "good"))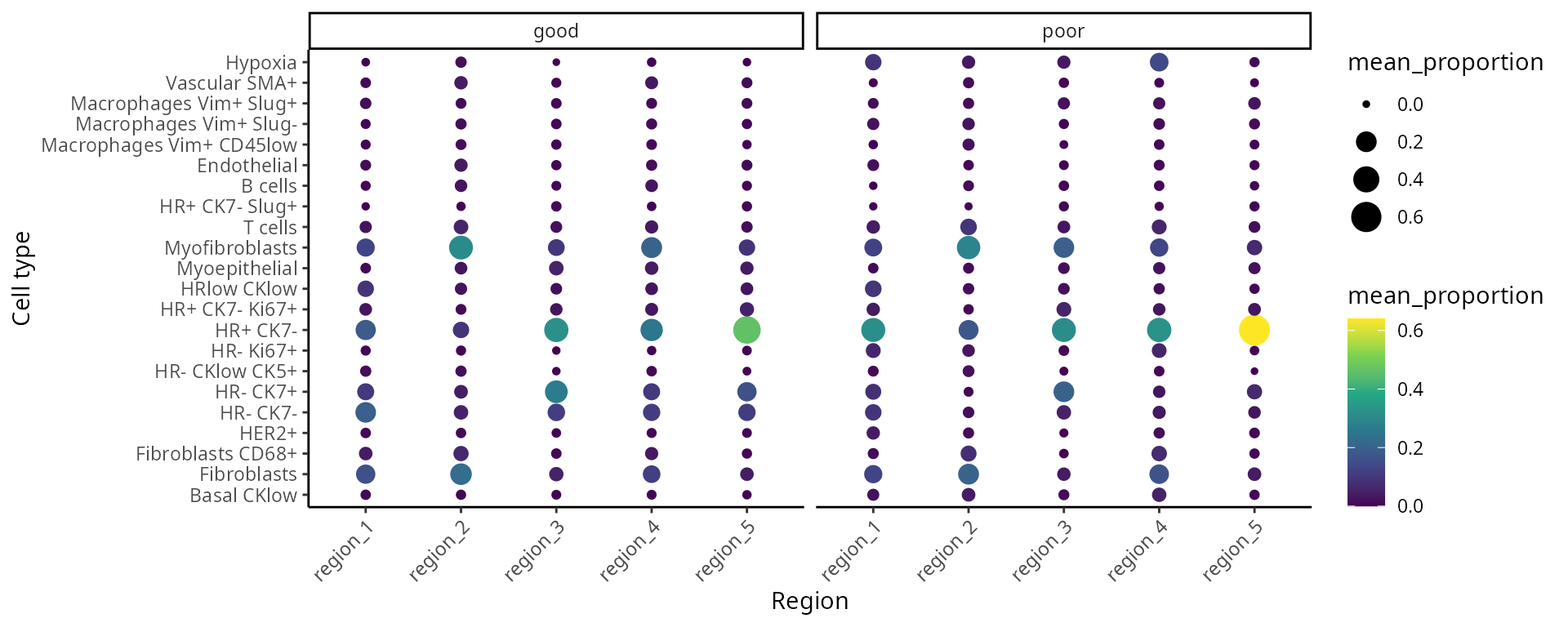

Interactive Q&A:

Q&A 3: Which regions appear to be different between poor prognosis (short-term survival) and good prognosis (long-term survival) individuals?

Further exploration by visualising selected regions

The number of sub-cell types increase considerably when we want to add spatial domain (region) information. To enhance clarity and facilitate understanding, it may be helpful to choose a predetermined region. The code generates a set of boxplots that enable the comparison of cell-type proportions between individuals with good and poor prognosis in region_5.

draw_selected_region_boxplot(data_sce, 
                             sample = "metabricId" , 
                             celltype ="description" , 
                             group  = "survivalgroup", 
                             group_of_interest =  c("poor" , "good"), 
                             select_region = "region_5")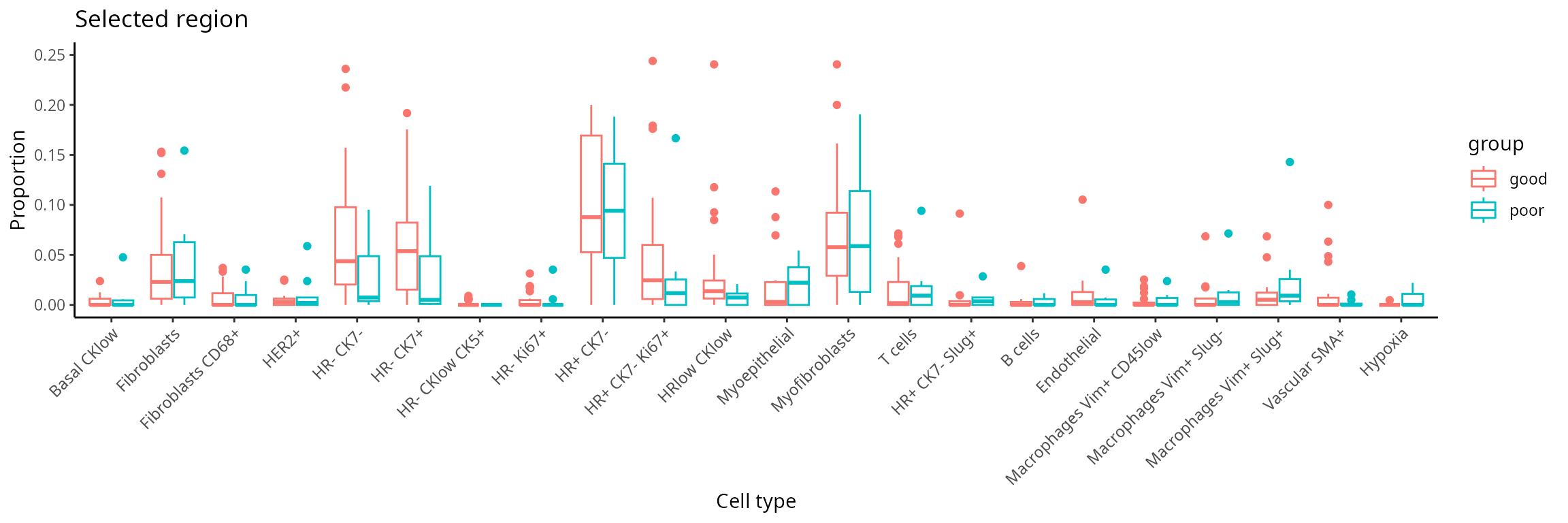

Part 3: Feature engineering with scFeatures

Here, we use scFeatures to generate molecular features for each individual using the features x cells matrices. These feature are interpretable and can be used for downstream analyses. In general, scFeatures generates features across six categories:

Cell-type proportions
Cell-type specific gene expressions
Cell-type specific pathway expressions
Cell-type interaction scores
Aggregated gene expressions
Spatial metrics: Nearest neighbour’s correlation, L statistics, and Moran’s I

The different types of features constructed enable a more comprehensive multi-view understanding of each individual. By default, the function will generate a total of 13 different types of features and are stored as 13 samples x features matrices, one for each feature type.

In additional to the spatial metrics, we can also consider region information as an additional layer of information. Thus, the following code aims to create cell-type specific features for each region. We use the function “paste0” to construct region-specific sub cell-types and name it as celltype in the R object data_sce. For simplicity, in this workshop, the variable celltype in the R object data_sce refers to region-specific sub-cell-types.

region <- data_sce$region

# Define a series of sub-cell-types that is regional specific
data_sce$celltype <- paste0( data_sce$description , "-" , region)

#print("Number of cells in samples")
#DT::datatable( data.frame(table( data_sce$metabricId )) , options = list(scrollX = TRUE))
df <- as.data.frame(table(data_sce$metabricId))
colnames(df) <- c("Sample", "Frequency")
df <- df[order(df$Frequency, decreasing = TRUE),]
df$Sample <- factor(df$Sample, levels = unique(df$Sample))
ggplot(df, aes(x = Sample, y = Frequency)) + geom_bar(stat = "identity") + theme(axis.text.x = element_text(angle = 45, hjust = 1, size = 5)) + labs(title = "Number of cells in samples", x = "\nSample", y = "Frequency\n")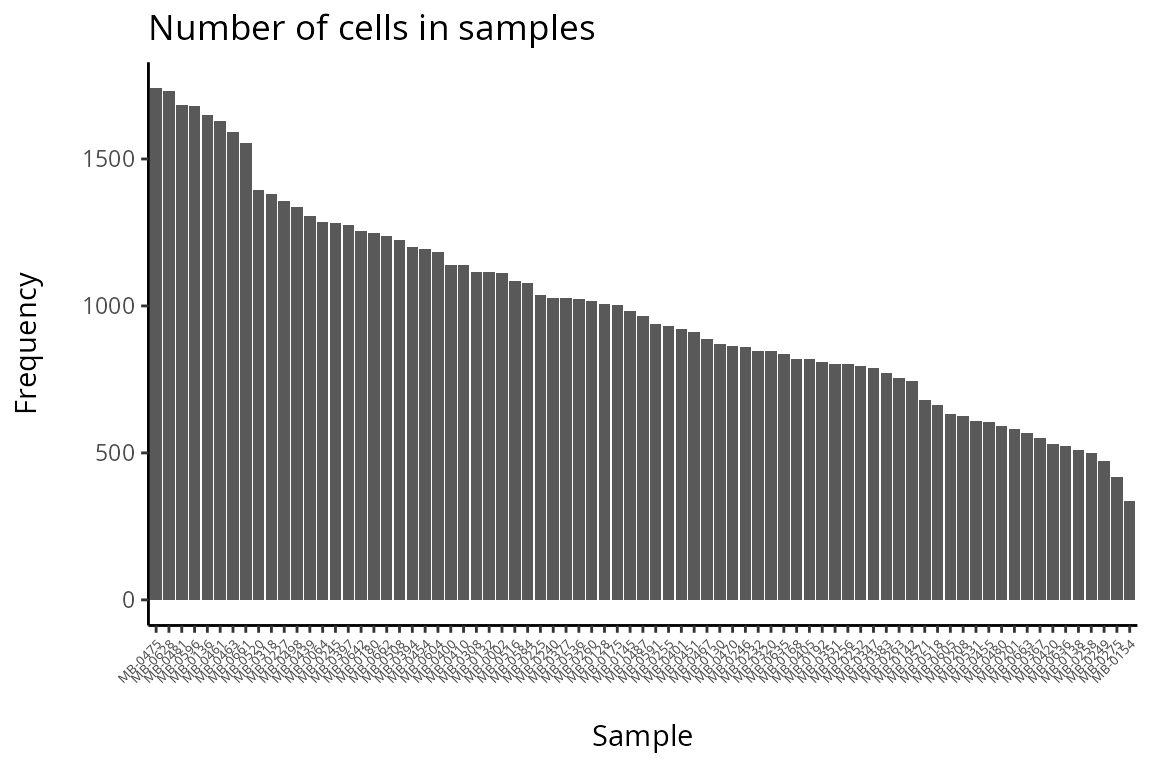

#print("Number of cells in each region-specific sub-cell-type")
# DT::datatable( data.frame(table(data_sce$celltype)) , options = list(scrollX = TRUE))
# hist(data_sce$celltype)

df <- as.data.frame(table(data_sce$celltype))
colnames(df) <- c("Sample", "Frequency")
df <- df[order(df$Frequency, decreasing = TRUE),]
df$Sample <- factor(df$Sample, levels = unique(df$Sample))
ggplot(df, aes(x = Sample, y = Frequency)) + geom_bar(stat = "identity") + theme(axis.text.x = element_text(angle = 45, hjust = 1, size = 5)) + labs(title = "Number of cells in each region x sub-cell-type", x = "\nCell-types", y = "Frequency\n")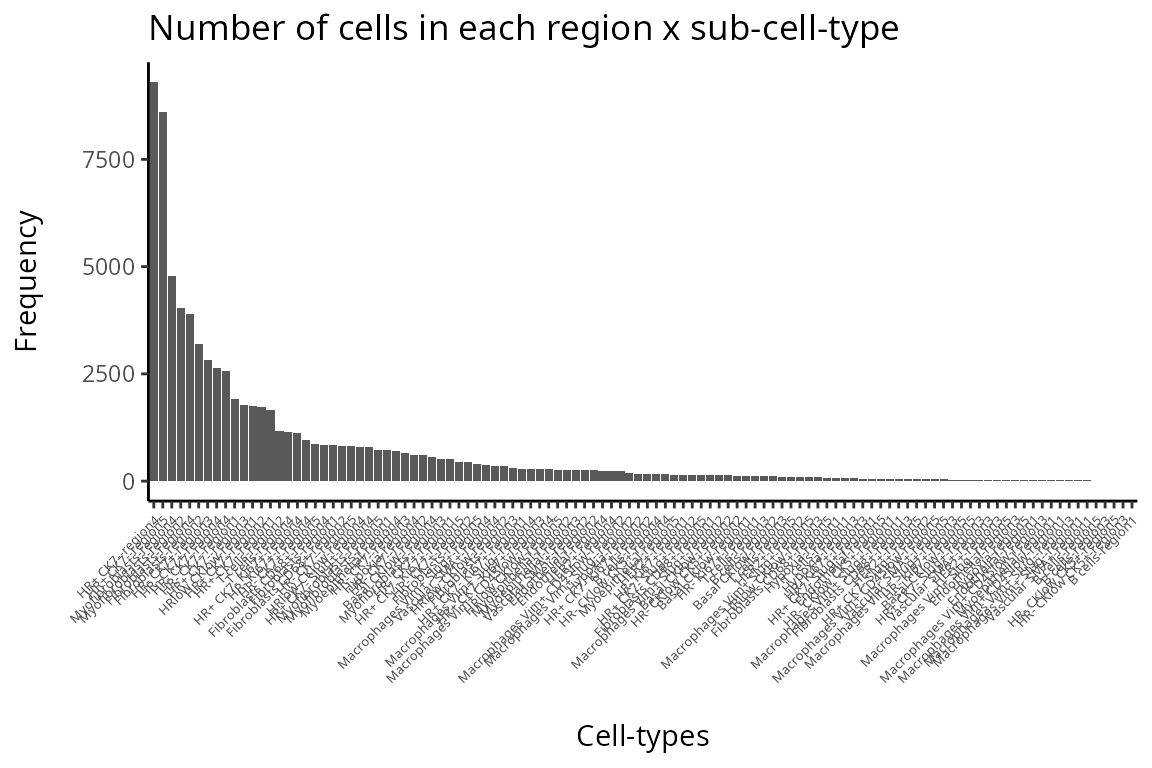

Discussion:

Q&A 4: Are there any samples or cell-types you would like to remove from the data?

3.1 How to create molecular representations of individuals?

There are different ways you can use scFeatures to generate molecular representations for individuals and it requires the following information for spatial data.

data,
sample,
X coordinates,
Y coordinates,
feature_types, and
type

There are a total of 13 different types of features (feature_types) that you can choose to generate. The argument type refers the type of input data we have. This is either scrna (single-cell RNA-sequencing data), spatial_p (spatial proteomics data), or spatial_t (single-cell spatial data).

Generate features

Suppose that we are interested in determining the proportion of cell-types within each region for each individual. It is necessary to specify type = spatial_p to reflect that we have spatial proteomics data and feature_types = proportion_raw to indicate we intend to calculate cell-type proportions for each of the region-specific cell-types.

## [A] The next few lines extract specific information from data_sce as input to scFeatures. 
## Extract the expression matrix from data_sce
IMCmatrix <- assay(data_sce)

## Extract the sample information 
## append the condition to the individuals so we can easily retrieve the individuals condition 
sample <- data_sce$metabricId 
cond  <- clinical[match(sample, clinical$metabricId), ]$survivalgroup
sample <- paste0(sample, "_cond_", cond ) 

## Extract the region-specific sub-cell-types
celltype <- data_sce$celltype

## Extract the spatial coordinates
spatialCoords <- list(colData(data_sce)$Location_Center_X, colData(data_sce)$Location_Center_Y)

### [B] Running scFeatures
scfeatures_result <- scFeatures(IMCmatrix, 
                                sample = sample, 
                                celltype = celltype, 
                                spatialCoords = spatialCoords,
                                feature_types = "proportion_raw", 
                                type = "spatial_p" )

The generated feature is a sample x feature matrix, the code below shows the first 5 features and the first 5 individuals for the region-specific sub-cell-types.

scfeatures_result$proportion_raw[1:5, 1:5]

##                      B cells-region1 B cells-region2 B cells-region3
## MB-0002_cond_neither    0.0000000000     0.000000000               0
## MB-0064_cond_neither    0.0000000000     0.000000000               0
## MB-0128_cond_good       0.0009950249     0.044776119               0
## MB-0130_cond_good       0.0000000000     0.000000000               0
## MB-0132_cond_neither    0.0000000000     0.007174888               0
##                      B cells-region4 B cells-region5
## MB-0002_cond_neither      0.00000000     0.000000000
## MB-0064_cond_neither      0.00000000     0.000000000
## MB-0128_cond_good         0.06666667     0.007960199
## MB-0130_cond_good         0.00000000     0.000000000
## MB-0132_cond_neither      0.00000000     0.000000000

Sub-cell-type

Suppose we are only interested in the molecular representation of HR- CK7+ within individuals within region 5.

## [A] The next few lines extract specific information from data_sce as input to scFeatures. 
## Select the HR- CK7+-region sub-cell-type 
index <-   grep("HR- CK7+-region" , data_sce$celltype, fixed=TRUE)
selected_data  <-  IMCmatrix[, index]
selected_sample <-  sample[index]
selected_celltype <- data_sce$celltype[ index] 
selected_spatialCoords <- list(colData(data_sce)$Location_Center_X[index], 
                               colData(data_sce)$Location_Center_Y[index])

### [B] Running scFeatures
scfeatures_result <- scFeatures( selected_data, 
                                 sample = selected_sample, 
                                 celltype = selected_celltype,
                                 spatialCoords = selected_spatialCoords,
                                 feature_types = "proportion_raw", type = "spatial_p" )

### [C] Visualize the regional composition makeup for each individual for HR- CK7+ and HR- CK7-
feature <- scfeatures_result$proportion_raw
feature <- feature[ grep("poor|good", rownames(feature)),  ]

plot_barplot(feature ) + ggtitle("Proportion raw feature") + labs(y = "proportion\n")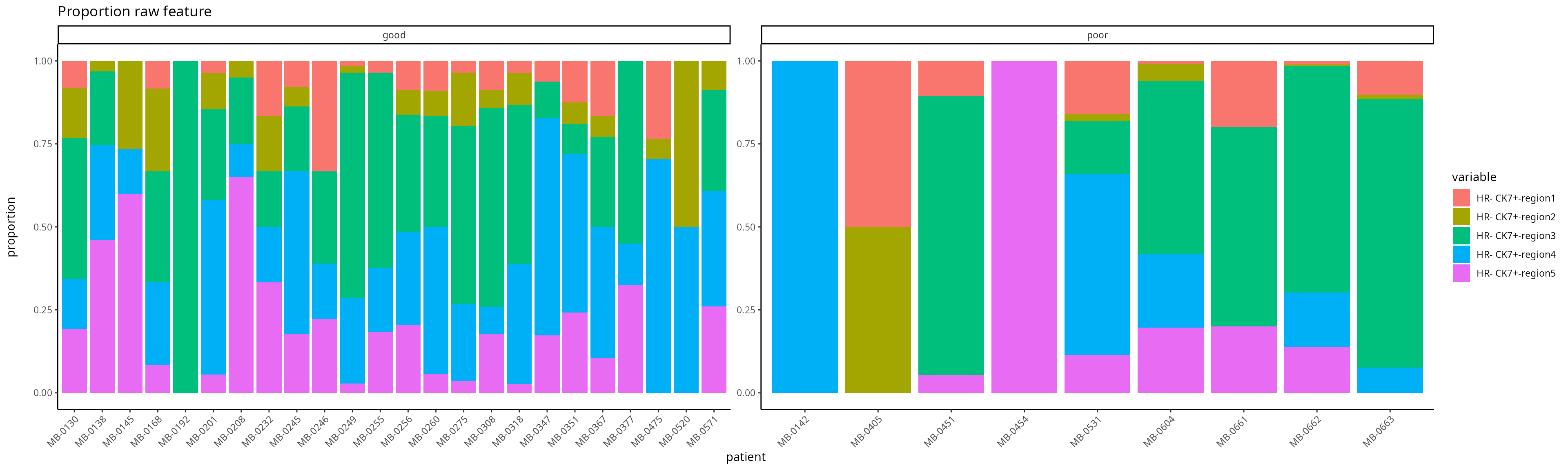

scFeatures code

The code below enable us to generate all feature types for all cell-types in a line. Due to limitations with today’s computational capacity, Please DO NOT run it in today’s workshop, it will crash your system.

# here, we specify that this is a spatial proteomics data
# scFeatures support parallel computation to speed up the process 
scfeatures_result <- scFeatures(IMCmatrix, 
                                type = "spatial_p",
                                sample = sample, 
                                celltype = celltype, 
                                spatialCoords = spatialCoords,
                                ncores = 32)

3.2: What can we learn from the outputs from scFeatures?

New features

Assuming you have already generated a collection of molecular representation for individuals, please load the prepared RDS file scfeatures_result.RDS. Again, you can remind yourself that all generated feature types are stored in a matrix of samples x features.

# Upload pre-generated RDS file
scfeatures_result <- readRDS("../../data/scfeatures_result.RDS")

# What are the features and the dimensions of features matrices that we have generated?
lapply(scfeatures_result, dim)

## $proportion_raw
## [1]  77 110
## 
## $proportion_logit
## [1]  77 110
## 
## $proportion_ratio
## [1]   77 5995
## 
## $gene_mean_celltype
## [1]   77 4180
## 
## $gene_prop_celltype
## [1]   77 4180
## 
## $gene_cor_celltype
## [1]    77 27958
## 
## $gene_mean_bulk
## [1] 77 38
## 
## $gene_prop_bulk
## [1] 77 38
## 
## $gene_cor_bulk
## [1]  77 703
## 
## $L_stats
## [1]   77 3842
## 
## $celltype_interaction
## [1]   77 4393
## 
## $morans_I
## [1] 77 38
## 
## $nn_correlation
## [1] 77 38

Association study

Can we identify “differential expression” for a feature of interest? The R object scfeatures_result contains a variety of features. A important question focuses on the identification of features that reflect an association with the prognostic outcome, specifically distinguishing between good and poor outcomes. The code provided below demonstrates the use of the limma() function to fit a linear model for the purpose of analysing gene_mean_celltype as an illustration feature type. The feature type known as gene_mean_celltype represents the mean protein expression for each sub-cell-type specific to a spatial region. It is a matrix consisting of 77 individuals and 4180 features. It is important to acknowledge that within the context of our IMC data, the term “gene” is used to refer to “protein”.

# Extract cell-type specific gene expression for all regions. 
gene_mean_celltype <- scfeatures_result$gene_mean_celltype

# Extract HR+ CK7 cell-type specific gene expression for Region5
index <-  grep( "HR+ CK7--region5", colnames(gene_mean_celltype) , fixed= T)
gene_mean_celltype <- gene_mean_celltype [, index] 

# transpose to ensure we have gene by sample matrix
gene_mean_celltype <- t(gene_mean_celltype)
      
# Extract the two conditions of interest - poor prognosis vs good prognosis
condition  <- unlist( lapply( strsplit( colnames(gene_mean_celltype) , "_cond_"), `[`, 2))
condition <- data.frame(sample = colnames(gene_mean_celltype), condition = condition )
select_index <- which( condition$condition %in% c("poor",  "good" ))
condition <- condition[ select_index, ]
gene_mean_celltype<- gene_mean_celltype [ ,  select_index]


# Calculate log fold change each protein using limma
design <- model.matrix(~condition, data = condition)
fit <- lmFit(gene_mean_celltype, design)
fit <- eBayes(fit)
tT <- topTable(fit, n = Inf)
tT$gene <- rownames(tT)
tT[1:6] <- signif(tT[1:6], digits=2)
DT::datatable(tT)

We visualise the comparison using a volcano plot and a dotplot for the cell-type specific expression feature. This is a type of scatter-plot that is used to quickly identify changes in large datasets and represent the significance (y-axis) versus effect size or fold-change (x-axis).

# The volcano plot - Significance vs Effect Size
ggplot( tT , aes(logFC,-log10(P.Value) , text = gene ) )+
      geom_point(aes(colour=-log10(P.Value)), alpha=1/3, size=1) +
      scale_colour_gradient(low="blue",high="red")+
      xlab("log2 fold change") + ylab("-log10 p-value")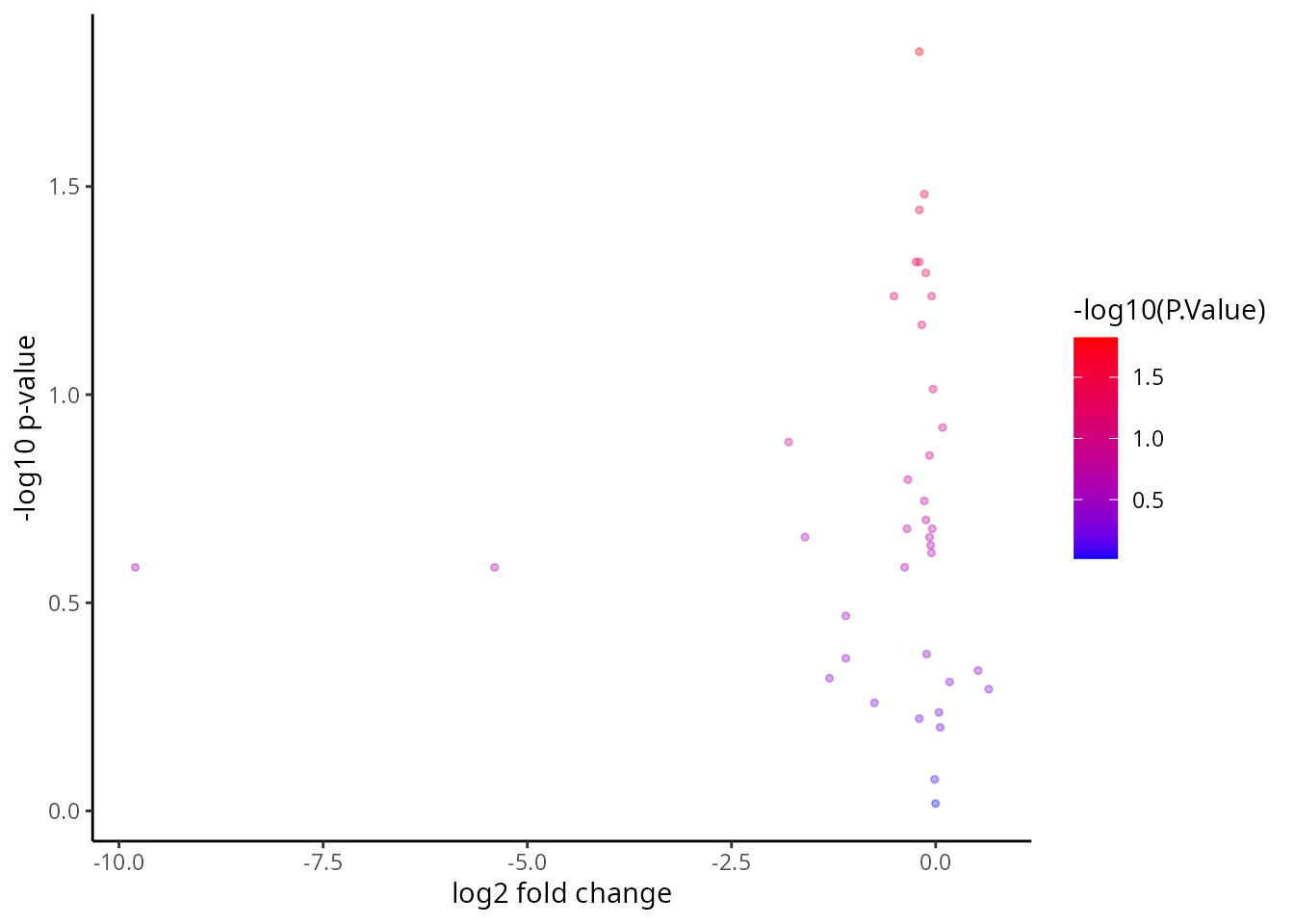

# order the proteins by log fold change 
tT <- tT[ order(tT$logFC, decreasing = T), ]
tT <- tT[1:20, ]
ggplot( tT , aes( y = reorder(gene, logFC) , x = logFC  ) )+
      geom_point(aes(colour=-log10(P.Value)), alpha=1/3, size=4) +
      scale_colour_gradient(low="blue",high="red")+
      xlab("logFC") + ylab("region specific cell type specfic features" )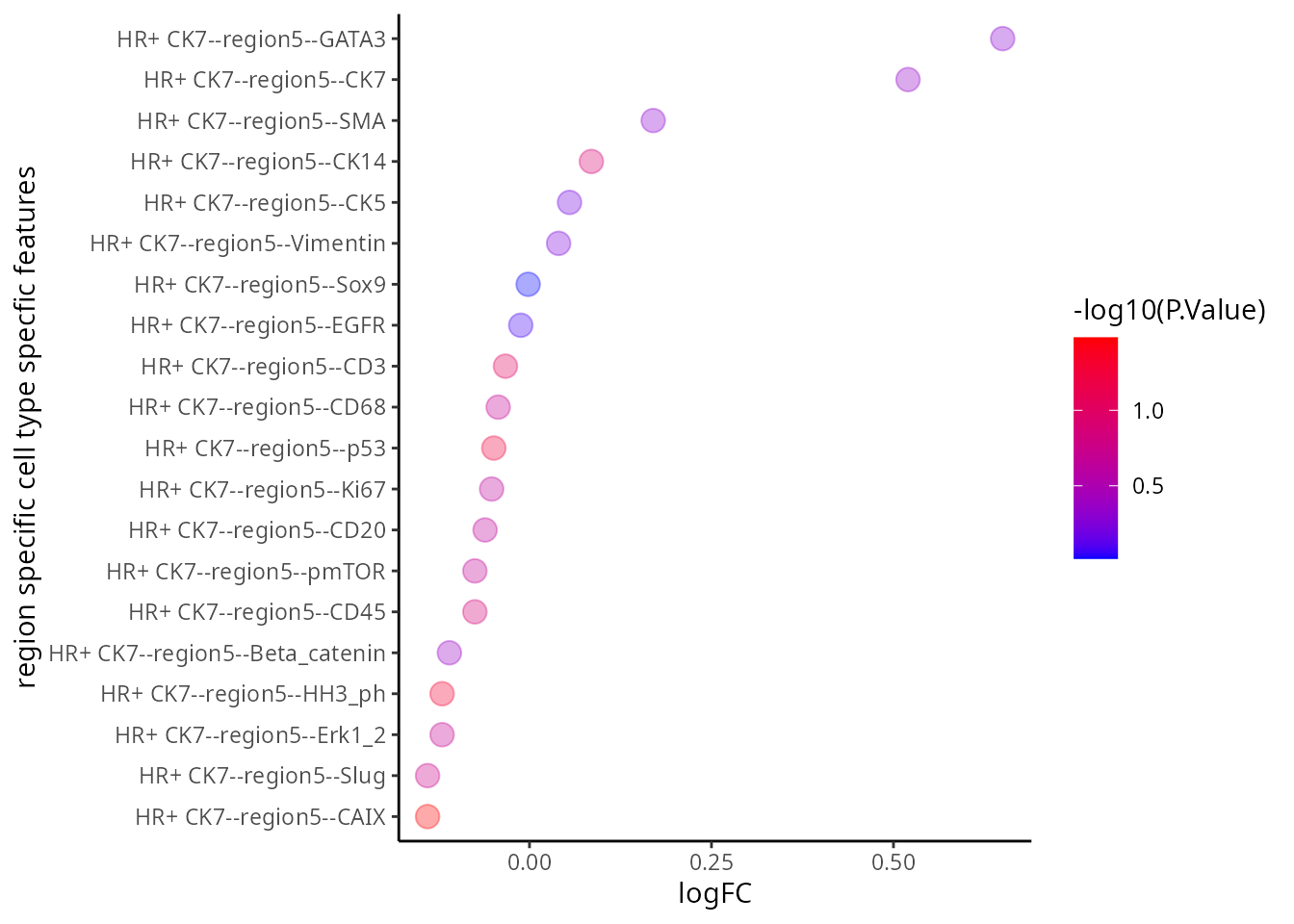

Interactive Q&A:

Q&A 5: Which figure do you prefer? The volcano plot or the dotplot?

Category-specific features

Can we identify the feature of interest among each type of feature category? In order to further develop our understanding of our data, it is important to bear in mind that the outcomes derived from scFeatures combine several association studies. Hence, it is necessary to examine every separate feature category as an individual unit of study. This section presents a graphic representation showing how to visualise the distribution of features across individuals. The following code has been developed to identify and retrieve all samples that have been associated to both good and poor prognosis. This particular step is necessary in this setting as our focus is limited to two specific categories of individuals rather than including all samples.

feature <- feature[ grep("poor|good", rownames(feature )),  ]

Gene mean cell-type

feature <- scfeatures_result$gene_mean_celltype
feature <- feature[ grep("poor|good", rownames(feature )),  ]
# Select the features from HR+ CK7--cell-type and in region 5
feature   <- feature[  , grep(  "HR+ CK7--region5" , colnames(feature) , fixed=T) ] 
plot_boxplot(feature) + ggtitle("Protein mean sub-cell-type feature")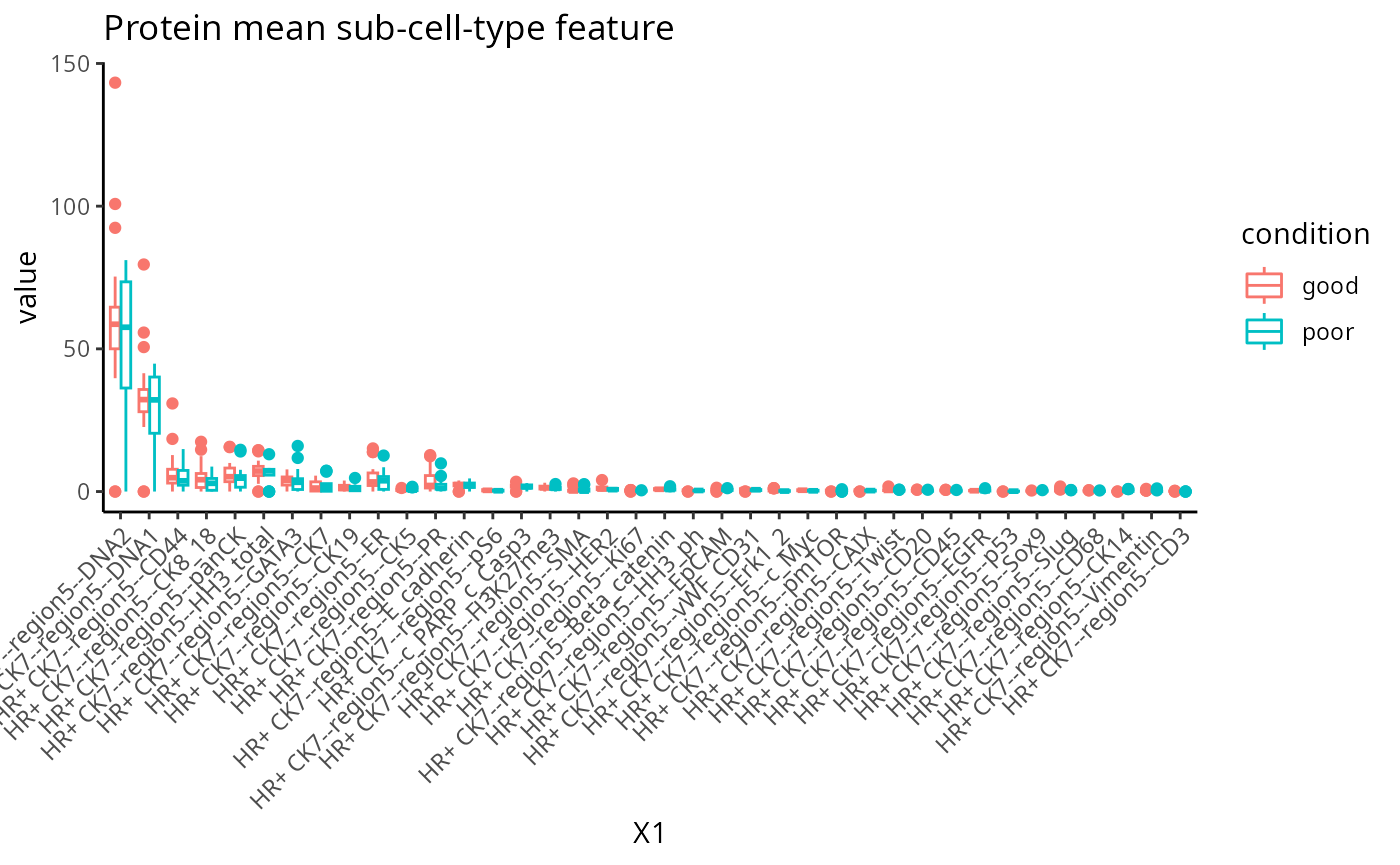

Gene mean bulk

feature <- scfeatures_result$gene_mean_bulk
feature <- feature[ grep("poor|good", rownames(feature )),  ]
plot_boxplot(feature) + ggtitle("Protein mean bulk feature")

Nearest neighbour correlation

feature <- scfeatures_result$nn_correlation
feature <- feature[ grep("poor|good", rownames(feature )),  ]
plot_boxplot(feature) + ggtitle("Nearest neighbour correlation feature")

Association study report

To accommodate for easier interpretation of the features, scFeatures contains a function run_association_study_report that enables the user to readily visualise and explore all generated features with one line of code. This should be used with caution as depending on the number of cell-types considered, some of the automatically-generated graphics may not be the most efficient way for interpretation.

In the code below we perform the following tasks:

Specify a folder to store the html report. Using the function getwd() we specify that we will store it in the current working directory.
A small for loop is created to select all the samples associated with good and poor prognosis and generate a new scfeatures_result. This step is only necessary if the comparison of interest is a subset of all your data.
Run the function run_association_study_report()

## Step 1 
output_folder <-  getwd()

## Step 2
scfeatures_result_new <- scfeatures_result
for (i in 1:13){
  thisfeature <- scfeatures_result[[i]]
  thisfeature <- thisfeature[ grep("poor|good", rownames(thisfeature )),]
  scfeatures_result_new[[i]] <- thisfeature
}

## Step 3
run_association_study_report(scfeatures_result_new, output_folder )

Part 4: Disease classification with ClassifyR

Recurrence risk estimation is a fundamental concern in medical research, particularly in the context of patient survival analysis. In this section, we will estimate recurrence risk using the molecular representation of individuals generated from scFeatures to build a survival model. We will use classifyR to build the survival model. The patient outcome is time-to-event, so, by default, ClassifyR will use Cox proportional hazards ranking to choose a set of features and also Cox proportional hazards to predict risk scores. We will also demonstrate other available models in ClassifyR.

Building a survival model

Recall in the previous section that we have stored the 13 matrices of different feature types in a list. Instead of manually retrieving each matrix from the list to build separate models, classifyR can directly take a list of matrices as an input and run a repeated cross-validation model on each matrix individually. Below, we run 5 repeats of 5-fold cross-validation. A high score indicates prognosis of a worse outcome than a lower risk score. Although we have provided the code below, to save time, just load the prepared RDS file classifyr_result_IMC.rds and we will focus on the interpretation in this workshop.

# We use the following variables:     
# timeRFS: "Time to Recurrence-Free Survival." It is the time period until recurrence occurs.    
# eventRFS: "Event in Recurrence-Free Survival."It indicates whether the event has occurred.    
# Breast.Tumour.Laterality: Laterality of tumors, eg, whether the tumor is located in left or right.     
# ER.Status: Whether the tumor is ER positive or ER negative.    
# Inferred.Menopausal.State: of the patient.    
# Grade: of the tumor.   
# Size: of the tumor.   

usefulFeatures <- c("Breast.Tumour.Laterality", "ER.Status", "Inferred.Menopausal.State", "Grade", "Size")
nFeatures <- append(list(clinical = 1:3), lapply(scfeatures_result, function(metaFeature) 1:5))
clinicalAndOmics <- append(list(clinical = clinical), scfeatures_result)

### generate classfyr result 
classifyr_result_IMC <- crossValidate(clinicalAndOmics, c("timeRFS", "eventRFS"),
                    extraParams = list(prepare = list(useFeatures = list(clinical = usefulFeatures))),
                    nFeatures = nFeatures, nFolds = 5, nRepeats = 5, nCores = 5)

classifyr_result_IMC <- readRDS("../../data/classifyr_result_IMC.rds")

Cox proportional hazards is a classical statistical method, as opposed to machine learning methods like Random survival forest. These machine learning methods can build remarkably complex relationships between features, however their running time can be much longer than Cox proportional hazards. We use feature selection to limit the number of features considered to at most 100 per metafeature and to save time, you can just load the prepared RDS file. We will compare the predictive performance between these methods.

nFeatures <- append(list(clinical = 1:3), lapply(scfeatures_result[2:length(scfeatures_result)], function(metaFeature) min(100, ncol(metaFeature))))
survForestCV <- crossValidate(clinicalAndOmics, outcome, nFeatures = nFeatures,
                classifier = "randomForest",
                nFolds = 5, nRepeats = 5, nCores = 5)

survForestCV <- readRDS("../../data/survForestCV.RDS")

Model performance

To examine the distribution of prognostic performance, use performancePlot. Currently, the only metric for time-to-event data is C-index and that will automatically be used because the predictive model type is tracked inside of the result objects.

## Make axis label 45 degree to improve readiability 
tilt <- theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust = 1))

## Putting two sets of cross-validation results together
multiresults <- append(classifyr_result_IMC, survForestCV)
ordering <- c("clinical", names(scfeatures_result))
performancePlot(multiresults,
                characteristicsList = list(x = "Assay Name", 
                                           row = "Classifier Name"),
                orderingList = list("Assay Name" = ordering)) + 
                tilt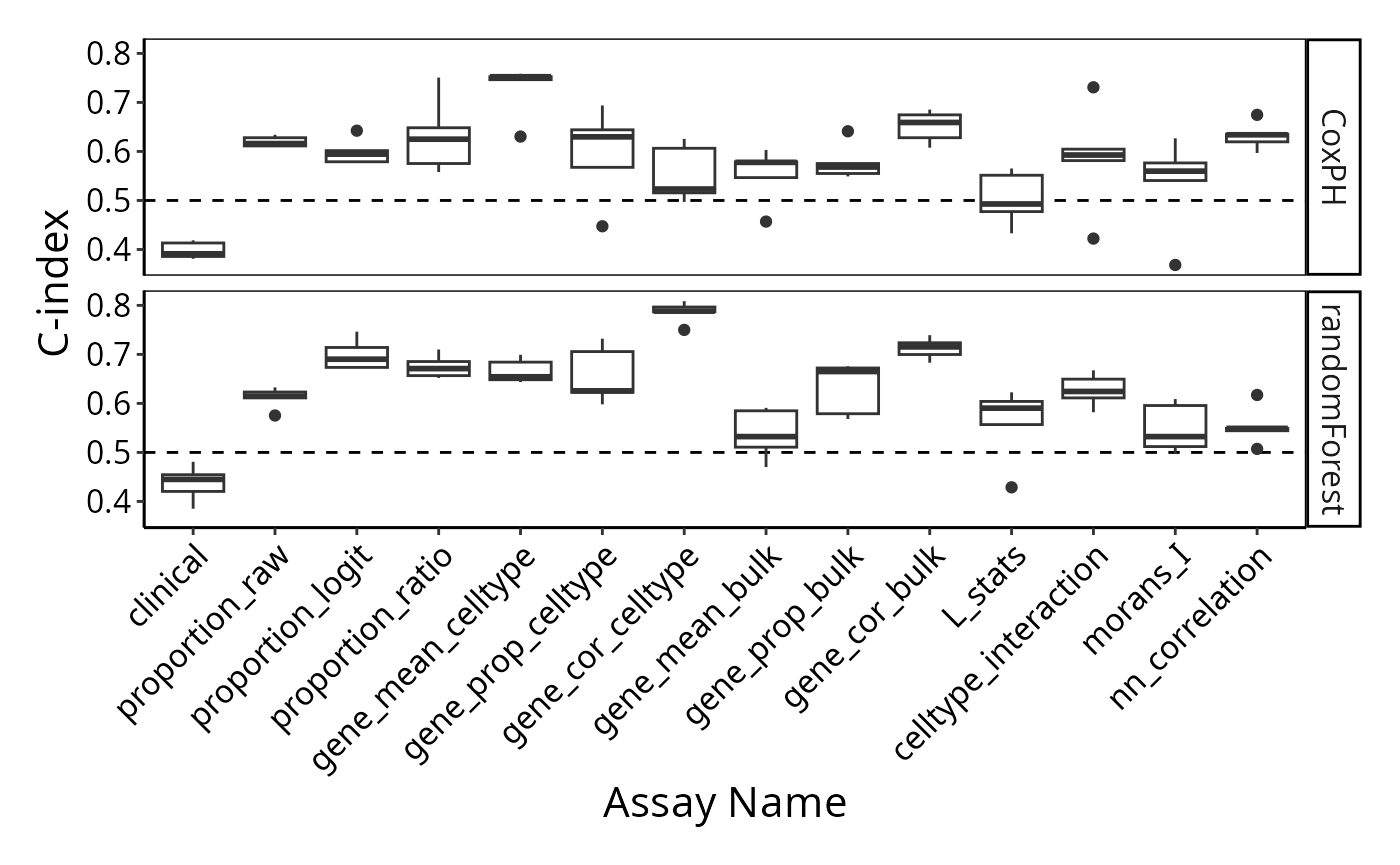

Note how the resultant plot is a ggplot2 object and can be further modified. The same code could be used for a categorical classifier because the random forest implementation provided by the ranger package has the same interface for both. We will examine feature selection stability with selectionPlot.

selectionPlot(multiresults,
                characteristicsList = list(x = "Assay Name", row = "Classifier Name"),
                orderingList = list("Assay Name" = ordering)) + tilt

distribution(classifyr_result_IMC[[1]], plot = FALSE)

##      assay                   feature proportion
## 1 clinical Inferred.Menopausal.State          1

A few samples are predicted better by some metafeatures than others.

The per-sample C-index is a metric unique to ClassifyR. Models and feature selection approaches may be seen in the vignette or listed by available().

Interactive Q&A:

Q&A 6: Is the highest predictive performance the only way to choose the best model or can other models be better for other reasons?

Cohort heterogeneity

Does each individual require a different collection of features? Using samplesMetricMap compare the per-sample C-index for Cox models for all kinds of metafeatures.

library(grid)
samplesMetricMap(classifyr_result_IMC)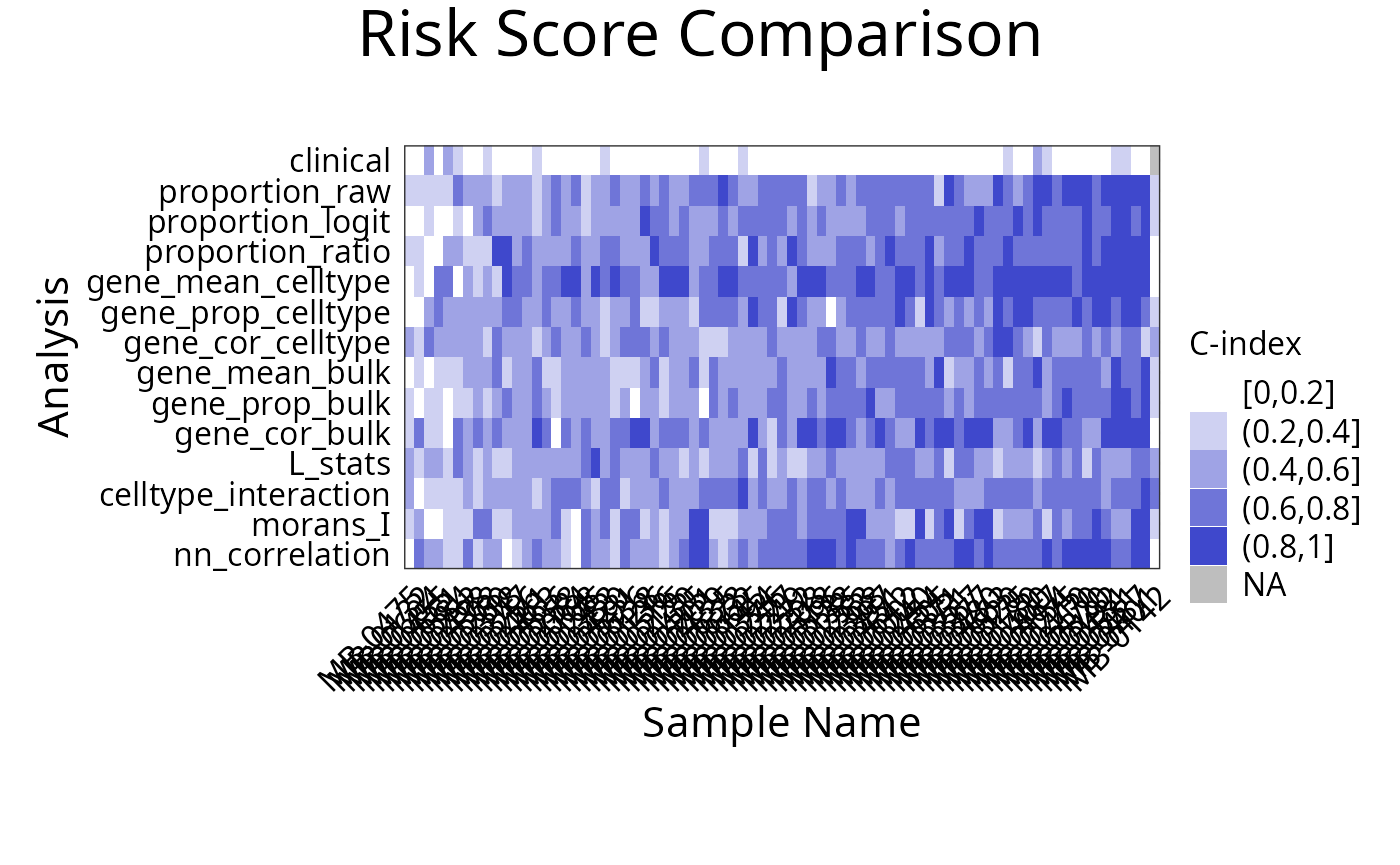

## TableGrob (2 x 1) "arrange": 2 grobs
##   z     cells    name                 grob
## 1 1 (2-2,1-1) arrange       gtable[layout]
## 2 2 (1-1,1-1) arrange text[GRID.text.5544]

Interactive Q&A:

Q&A 7: Are spatial features important for predicting recurrence? Does it hold for all individuals?

Appendix

Explanation of spatial features

L function:

The L function is a spatial statistic used to assess the spatial distribution of cell-types. It assesses the significance of cell-cell interactions, by calculating the density of a cell-type with other cell-types within a certain radius. High values indicate spatial association (co-localisation), low values indicate spatial avoidance.

tableau_palette <- scale_colour_tableau( palette = "Tableau 20")
color_codes <- tableau_palette$palette(10)
# select one patient 
one_sample  <- data_sce[ , data_sce$metabricId == "MB-0128"  ]
one_sample <- data.frame( colData(one_sample) )

one_sample$celltype <- one_sample$description

# select certain cell types to examine the interaction 
index <-  one_sample$celltype  %in% c("B cells", "Fibroblasts")
one_sample$celltype[!index] <- "others"
a <-ggplot( one_sample, aes(x = Location_Center_X , y = Location_Center_Y, colour = celltype )) + geom_point()  + scale_colour_manual(values = color_codes)  + ggtitle( "Patient MB-0128 - high L value with \n B cells interacting Fibroblasts")
 

one_sample$celltype <- one_sample$description
index <-  one_sample$celltype  %in% c("Fibroblasts", "HR- CK7-")
one_sample$celltype[!index] <- "others"
b <- ggplot( one_sample, aes(x = Location_Center_X , y = Location_Center_Y, colour = celltype )) + geom_point()  + scale_colour_manual(values = color_codes)  + ggtitle( "Patient MB-0128 - low L value with \n B cells interacting HR_ CK7")
 
ggarrange(plotlist = list(a,b))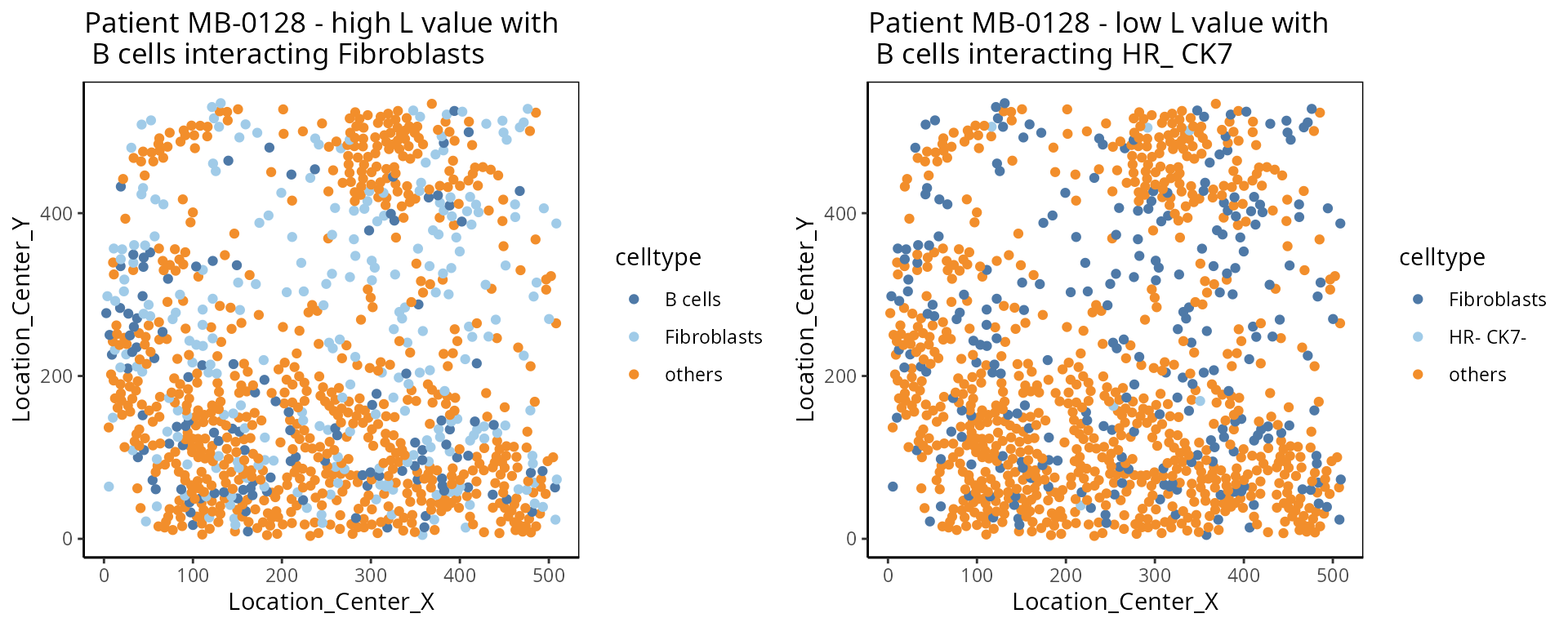

Cell type interaction composition:

We calculate the nearest neighbours of each cell and then calculate the pairs of cell-types based on the nearest neighbour. This allows us to summarise it into a cell-type interaction composition.

one_sample  <- data_sce[ , data_sce$metabricId == "MB-0263"  ]
one_sample <- data.frame( colData(one_sample) )

one_sample$celltype <- one_sample$description
 
a <-ggplot( one_sample, aes(x = Location_Center_X , y = Location_Center_Y, colour = celltype )) + geom_point()  + scale_colour_manual(values = color_codes)  + ggtitle("Patient MB-0263")


feature  <- scfeatures_result$celltype_interaction
to_plot <- data.frame( t( feature[ "MB-0263_cond_poor" , ])  )
to_plot$feature <- rownames(to_plot) 
colnames(to_plot) <- c("value", "celltype interaction composition")
 
to_plot <- to_plot[ order(to_plot$value, decreasing = T), ]
to_plot <- to_plot[1:10, ]
to_plot$`celltype interaction composition` <- factor(to_plot$`celltype interaction composition`, levels = to_plot$`celltype interaction composition`)

b <- ggplot(to_plot, aes(x =  `celltype interaction composition`  ,  y = value, fill=`celltype interaction composition`)) + geom_bar(stat="identity" ) + ylab("Major cell-type interactions")  +
  theme(axis.text.x = element_text(angle = 45, vjust = 1, hjust=1)) 

ggarrange(plotlist = list(a,b))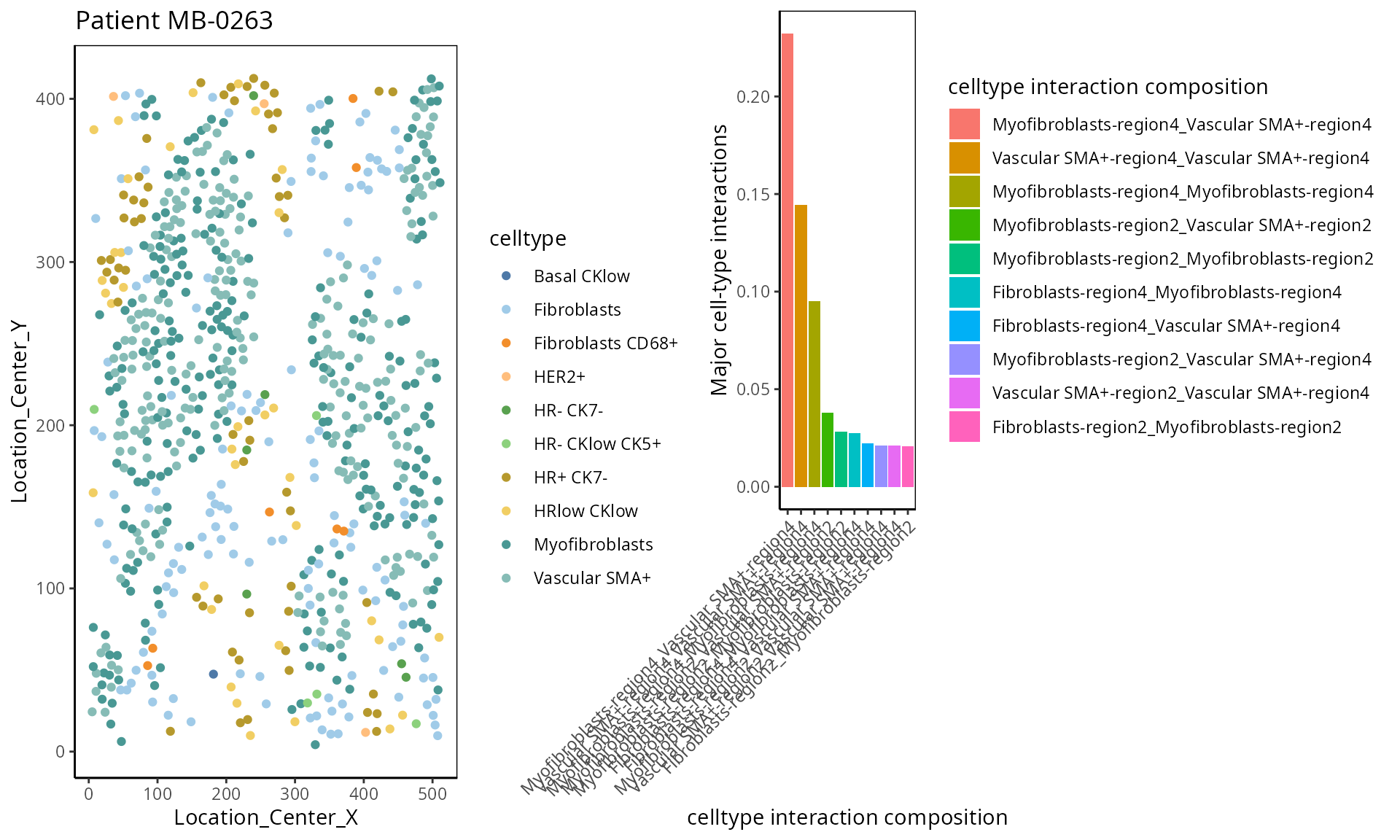

Moran’s I:

Moran’s I is a spatial autocorrelation statistic based on both location and values. It quantifies whether similar values tend to occur near each other or are dispersed.

high  <- data_sce["Ki67", data_sce$metabricId == "MB-0132"  ]
high_meta <- data.frame( colData(high) ) 
high_meta$expression <- as.vector(logcounts( high)) 

low  <- data_sce["Ki67",  data_sce$metabricId == "MB-0249" ]
low_meta <- data.frame( colData(low) )
low_meta$expression <- as.vector(logcounts(low))


a <- ggplot(high_meta, aes(x = Location_Center_X , y = Location_Center_Y, colour =expression)) + geom_point(alpha=0.5) + scale_colour_viridis_c() + ggtitle("Patient MB-0132 - high Moran's I in Ki67")

b <- ggplot(low_meta, aes(x = Location_Center_X , y = Location_Center_Y, colour =expression)) + geom_point(alpha=0.5) + scale_colour_viridis_c() + ggtitle("Patient MB-0249 - low Moran's I in Ki67")

ggarrange(plotlist = list(a,b))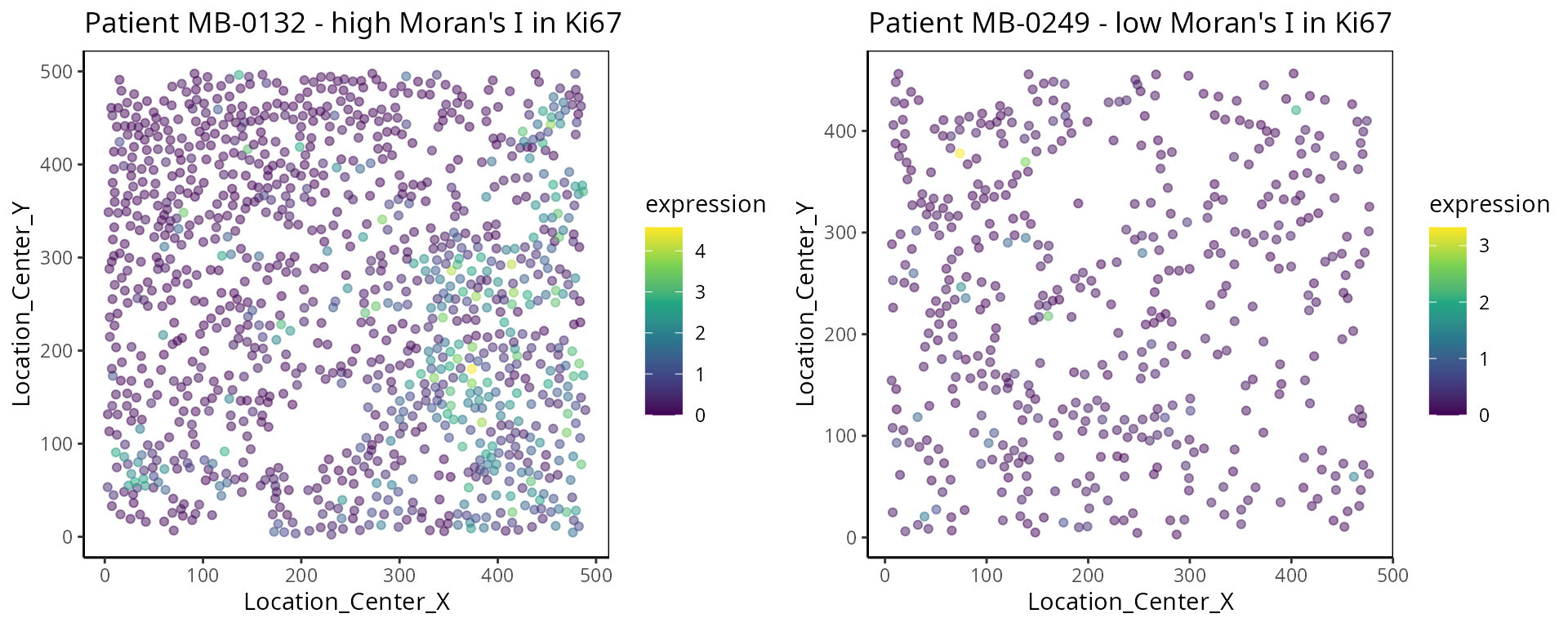

Nearest Neighbor Correlation:

This metric measures the correlation of proteins/genes between a cell and its nearest neighbour cell.

 plot_nncorrelation <- function(thissample , thisprotein){
   
       sample_name <- thissample
       thissample <- data_sce[, data_sce$metabricId ==     sample_name]
    
      
      exprsMat <- logcounts(thissample)
     
    # calculate NN correlation 
    cell_points_cts <- spatstat.geom::ppp(
            x = as.numeric(thissample$Location_Center_X ), y = as.numeric(thissample$Location_Center_Y),
            check = FALSE,
            xrange = c(
                min(as.numeric(thissample$Location_Center_X)),
                max(as.numeric(thissample$Location_Center_X))
            ),
            yrange = c(
                min(as.numeric(thissample$Location_Center_Y)),
                max(as.numeric(thissample$Location_Center_Y))
            ),
            marks = t(as.matrix(exprsMat))
        )
    
     value <-  spatstat.explore::nncorr(cell_points_cts)["correlation", ]
      value <-  value[  thisprotein]
     
    # Find the indices of the two nearest neighbors for each cell
    nn_indices <- nnwhich(cell_points_cts, k = 1)
    
    protein <-  thisprotein
    df <- data.frame(thiscell_exprs  = exprsMat[protein, ] , exprs =  exprsMat[protein,nn_indices ])
    
   p <-  ggplot(df, aes( x =thiscell_exprs ,  y = exprs , colour =  exprs  )) +
      geom_point(alpha = 0.3) + ggtitle(paste0( "Patient ", sample_name ,  " nn_corr = " ,  round(value, 2)  )) + scale_colour_viridis_c() + xlab("This cell expression") + ylab("Neighbouring cell expression")
   
   return (p ) 

}

    
p1 <- plot_nncorrelation("MB-0605",  "HER2")
p2 <- plot_nncorrelation("MB-0258",  "HER2")

ggarrange(plotlist = list(p1, p2))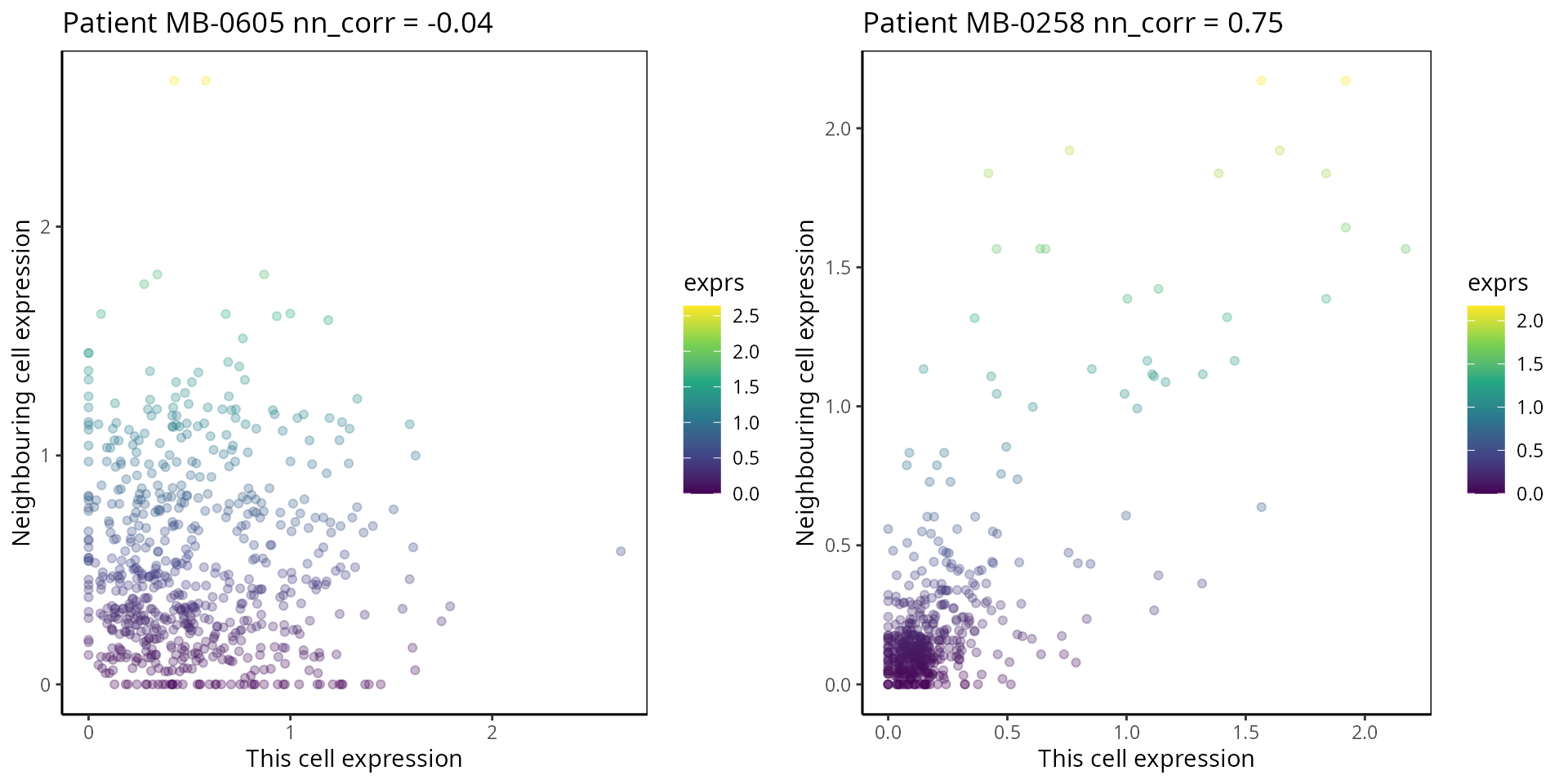

SessionInfo

sessionInfo()

## R version 4.4.1 (2024-06-14)
## Platform: x86_64-pc-linux-gnu
## Running under: Debian GNU/Linux 12 (bookworm)
## 
## Matrix products: default
## BLAS:   /usr/lib/x86_64-linux-gnu/openblas-pthread/libblas.so.3 
## LAPACK: /usr/lib/x86_64-linux-gnu/openblas-pthread/libopenblasp-r0.3.21.so;  LAPACK version 3.11.0
## 
## locale:
##  [1] LC_CTYPE=C.UTF-8       LC_NUMERIC=C           LC_TIME=C.UTF-8       
##  [4] LC_COLLATE=C.UTF-8     LC_MONETARY=C.UTF-8    LC_MESSAGES=C.UTF-8   
##  [7] LC_PAPER=C.UTF-8       LC_NAME=C              LC_ADDRESS=C          
## [10] LC_TELEPHONE=C         LC_MEASUREMENT=C.UTF-8 LC_IDENTIFICATION=C   
## 
## time zone: Australia/Sydney
## tzcode source: system (glibc)
## 
## attached base packages:
## [1] grid      stats4    stats     graphics  grDevices utils     datasets 
## [8] methods   base     
## 
## other attached packages:
##  [1] reshape_0.8.9               scran_1.32.0               
##  [3] scater_1.32.0               scuttle_1.14.0             
##  [5] spatstat_3.1-1              spatstat.linnet_3.2-1      
##  [7] spatstat.model_3.3-1        rpart_4.1.23               
##  [9] spatstat.explore_3.3-2      nlme_3.1-165               
## [11] spatstat.random_3.3-1       spatstat.geom_3.3-2        
## [13] spatstat.univar_3.0-0       spatstat.data_3.1-2        
## [15] survminer_0.4.9             ggpubr_0.6.0               
## [17] tidyr_1.3.1                 scattermore_1.2            
## [19] plotly_4.10.4               limma_3.60.2               
## [21] dplyr_1.1.4                 spicyR_1.19.2              
## [23] ggthemes_5.1.0              lisaClust_1.12.3           
## [25] ClassifyR_3.9.1             survival_3.6-4             
## [27] BiocParallel_1.38.0         MultiAssayExperiment_1.30.0
## [29] generics_0.1.3              scFeatures_1.4.0           
## [31] ggplot2_3.5.1               SingleCellExperiment_1.26.0
## [33] SummarizedExperiment_1.34.0 Biobase_2.64.0             
## [35] GenomicRanges_1.56.0        GenomeInfoDb_1.40.1        
## [37] IRanges_2.38.0              S4Vectors_0.42.0           
## [39] BiocGenerics_0.50.0         MatrixGenerics_1.16.0      
## [41] matrixStats_1.3.0          
## 
## loaded via a namespace (and not attached):
##   [1] fs_1.6.4                   ProtGenerics_1.36.0       
##   [3] GSVA_1.52.0                spatstat.sparse_3.1-0     
##   [5] bitops_1.0-7               httr_1.4.7                
##   [7] RColorBrewer_1.1-3         numDeriv_2016.8-1.1       
##   [9] EnsDb.Hsapiens.v79_2.99.0  tools_4.4.1               
##  [11] backports_1.5.0            DT_0.33                   
##  [13] utf8_1.2.4                 R6_2.5.1                  
##  [15] HDF5Array_1.32.0           uwot_0.2.2                
##  [17] mgcv_1.9-1                 lazyeval_0.2.2            
##  [19] rhdf5filters_1.16.0        withr_3.0.0               
##  [21] gridExtra_2.3              coxme_2.2-22              
##  [23] cli_3.6.2                  textshaping_0.3.7         
##  [25] labeling_0.4.3             sass_0.4.9                
##  [27] survMisc_0.5.6             SingleCellSignalR_1.16.0  
##  [29] pkgdown_2.0.9              Rsamtools_2.20.0          
##  [31] systemfonts_1.0.6          ggupset_0.3.0             
##  [33] R.utils_2.12.3             rstudioapi_0.16.0         
##  [35] RSQLite_2.3.6              shape_1.4.6.1             
##  [37] BiocIO_1.14.0              crosstalk_1.2.1           
##  [39] gtools_3.9.5               car_3.1-2                 
##  [41] scam_1.2-16                Matrix_1.7-0              
##  [43] ggbeeswarm_0.7.2           fansi_1.0.6               
##  [45] abind_1.4-5                R.methodsS3_1.8.2         
##  [47] lifecycle_1.0.4            yaml_2.3.8                
##  [49] edgeR_4.2.0                carData_3.0-5             
##  [51] gplots_3.1.3.1             rhdf5_2.48.0              
##  [53] SparseArray_1.4.0          Rtsne_0.17                
##  [55] blob_1.2.4                 dqrng_0.4.1               
##  [57] bdsmatrix_1.3-7            crayon_1.5.2              
##  [59] lattice_0.22-6             cowplot_1.1.3             
##  [61] beachmat_2.20.0            msigdbr_7.5.1             
##  [63] GenomicFeatures_1.56.0     annotate_1.82.0           
##  [65] KEGGREST_1.44.0            magick_2.8.3              
##  [67] pillar_1.9.0               knitr_1.46                
##  [69] metapod_1.12.0             boot_1.3-30               
##  [71] rjson_0.2.21               codetools_0.2-20          
##  [73] glue_1.7.0                 V8_4.4.2                  
##  [75] data.table_1.15.4          vctrs_0.6.5               
##  [77] png_0.1-8                  gtable_0.3.5              
##  [79] cachem_1.0.8               xfun_0.43                 
##  [81] S4Arrays_1.4.1             pheatmap_1.0.12           
##  [83] iterators_1.0.14           KMsurv_0.1-5              
##  [85] statmod_1.5.0              bluster_1.14.0            
##  [87] bit64_4.0.5                RcppAnnoy_0.0.22          
##  [89] bslib_0.7.0                irlba_2.3.5.1             
##  [91] vipor_0.4.7                KernSmooth_2.23-24        
##  [93] colorspace_2.1-0           DBI_1.2.3                 
##  [95] tidyselect_1.2.1           proxyC_0.4.1              
##  [97] bit_4.0.5                  compiler_4.4.1            
##  [99] curl_5.2.1                 AUCell_1.26.0             
## [101] graph_1.82.0               BiocNeighbors_1.22.0      
## [103] desc_1.4.3                 DelayedArray_0.30.0       
## [105] rtracklayer_1.64.0         scales_1.3.0              
## [107] caTools_1.18.2             stringr_1.5.1             
## [109] SpatialExperiment_1.14.0   digest_0.6.35             
## [111] goftest_1.2-3              minqa_1.2.7               
## [113] spatstat.utils_3.1-0       rmarkdown_2.26            
## [115] XVector_0.44.0             htmltools_0.5.8.1         
## [117] pkgconfig_2.0.3            lme4_1.1-35.3             
## [119] sparseMatrixStats_1.16.0   highr_0.10                
## [121] fastmap_1.2.0              ensembldb_2.28.0          
## [123] rlang_1.1.4                GlobalOptions_0.1.2       
## [125] htmlwidgets_1.6.4          UCSC.utils_1.0.0          
## [127] DelayedMatrixStats_1.26.0  farver_2.1.2              
## [129] ggh4x_0.2.8                jquerylib_0.1.4           
## [131] zoo_1.8-12                 jsonlite_1.8.8            
## [133] R.oo_1.26.0                BiocSingular_1.20.0       
## [135] RCurl_1.98-1.14            magrittr_2.0.3            
## [137] GenomeInfoDbData_1.2.12    Rhdf5lib_1.26.0           
## [139] munsell_0.5.1              Rcpp_1.0.12               
## [141] viridis_0.6.5              ggnewscale_0.4.10         
## [143] ape_5.8                    babelgene_22.9            
## [145] stringi_1.8.3              zlibbioc_1.50.0           
## [147] MASS_7.3-60.2              plyr_1.8.9                
## [149] ggrepel_0.9.5              parallel_4.4.1            
## [151] deldir_2.0-4               Biostrings_2.72.0         
## [153] splines_4.4.1              tensor_1.5                
## [155] multtest_2.60.0            circlize_0.4.16           
## [157] locfit_1.5-9.9             igraph_2.0.3              
## [159] ggsignif_0.6.4             reshape2_1.4.4            
## [161] ScaledMatrix_1.12.0        XML_3.99-0.16.1           
## [163] evaluate_0.23              BiocManager_1.30.23       
## [165] nloptr_2.0.3               tweenr_2.0.3              
## [167] foreach_1.5.2              EnsDb.Mmusculus.v79_2.99.0
## [169] purrr_1.0.2                polyclip_1.10-6           
## [171] km.ci_0.5-6                ggforce_0.4.2             
## [173] rsvd_1.0.5                 broom_1.0.5               
## [175] xtable_1.8-4               restfulr_0.0.15           
## [177] AnnotationFilter_1.28.0    rstatix_0.7.2             
## [179] viridisLite_0.4.2          class_7.3-22              
## [181] ragg_1.3.0                 tibble_3.2.1              
## [183] lmerTest_3.1-3             beeswarm_0.4.0            
## [185] memoise_2.0.1              AnnotationDbi_1.66.0      
## [187] GenomicAlignments_1.40.0   cluster_2.1.6             
## [189] concaveman_1.1.0           GSEABase_1.66.0

Acknowledgment

The authors thank all their colleagues, particularly at The University of Sydney, Sydney Precision Data Science and Charles Perkins Centre for their support and intellectual engagement. Special thanks to Ellis Patrick, Shila Ghazanfar, Andy Tran, Helen, and Daniel for guiding and supporting the building of this workshop.

Yue Cao, Andy Tran, Daniel Kim, Dario Strbenac, Nicholas Robertson, Helen Fu, Jean Yang

24 July, 2024

Overview

Preparation and assumed knowledge

Learning Objectives

Time outline

Part 2: Exploring spatial data

Data and background

Covariates

Summary

Visualise data

Spatial structure

Cellular neighbourhoods

Individual level

Across individuals

Further exploration by visualising selected regions

Part 3: Feature engineering with scFeatures

3.1 How to create molecular representations of individuals?

Generate features

Sub-cell-type

scFeatures code

3.2: What can we learn from the outputs from scFeatures?

New features

Association study

Category-specific features

Gene mean cell-type

Gene mean bulk

Nearest neighbour correlation

Association study report

Part 4: Disease classification with ClassifyR

Building a survival model

Model performance

Cohort heterogeneity

Appendix

Explanation of spatial features

SessionInfo

Acknowledgment